排序算法总结

趁着有时间把学习过的排序算法又实现了一遍复习一下，实现的排序算法主要有以下几种：冒泡排序、快速排序，选择排序，堆排序，插入排序，合并排序，希尔排序，桶排序等。

下面是网上找的一张图片，总结了常见排序算法的时间复杂度、空间复杂度以及稳定性，可以参考一下。

 

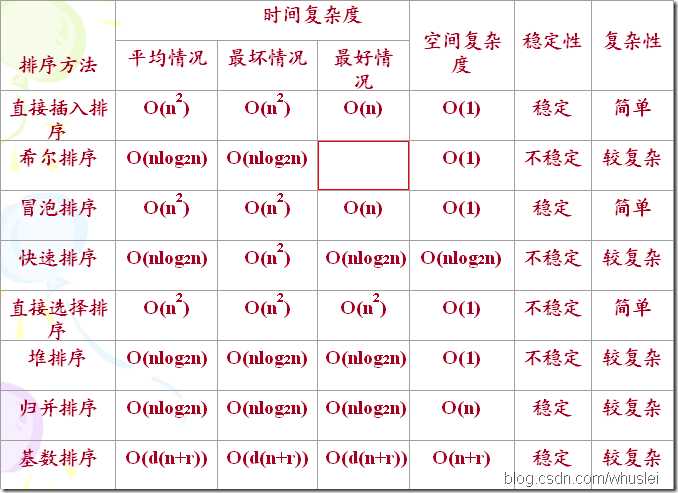
下面排序的都是vector<int>,懒得写模板了

1.冒泡排序

冒泡排序是最简单的排序算法，冒泡排序的基本思想是从后往前（或从前往后）两两比较相邻元素的值，若为逆序，则交换它们，直到序列比较完。我们称它为一趟冒泡。每一趟冒泡都会将一个元素放置到其最终位置上。

//冒泡排序
void BubbleSort(vector<int> &vec)
{
    int n = vec.size();
    for (int i = 0; i < n; ++i)
        for (int j = n - 1; j > i; --j)
        {
            if (vec[j] < vec[j - 1])
            {
                int tmp = vec[j];
                vec[j] = vec[j - 1];
                vec[j - 1] = tmp;
            }
        }
}

 

2.快速排序

快速排序是对冒泡排序的一种改进。其基本思想是基于分治法：在待排序表L[n]中任取一个元素pivot作为基准，通过一趟排序将序列划分为两部分L[1...K-1]和L[k+1...n]，是的L[1...k-1]中的所有元素都小于pivot，而L[k+1...n]中所有元素都大于或等于pivot。则pivot放在了其最终位置L(k)上。然后，分别递归地对两个子序列重复上述过程，直至每部分内只有一个元素或空为止，即所有元素放在了其最终位置上。

//划分为两个部分
int Partition(vector<int> &vec, int left, int right)
{
    int base = vec[left];
    while (left < right)
    {    
        while (left < right && vec[right] >= base)//从右向左找到第一个小于base值的元素
            --right;
        vec[left] = vec[right];//将比base值小的数移动到左边
        while (left < right && vec[left] <= base)//从左向右找到第一个大于base值的元素
            ++left;
        vec[right] = vec[left];
    }
    vec[left] = base;
    return left;
}

void QuickSort(vector<int> &vec, int left, int right)
{
    if (left < right)//递归跳出的条件
    {
        int pos = Partition(vec, left, right);
        QuickSort(vec, left, pos - 1);
        QuickSort(vec, pos + 1, right);
    }
}

 

 3.简单选择排序

对要排序的序列，选出关键字最小的数据，将它和第一个位置的数据交换，接着，选出关键字次小的数据，将它与第二个位置上的数据交换。以此类推，直到完成整个过程。

所以如果有n个数据，那么则需要遍历n-1遍。

void SelectSort(vector<int> &vec)
{
    int n = vec.size();
    for (int i = 0; i < n - 1; ++i)
    {
        int minPos = i;
        //查找最小值
        for (int j = i + 1; j < n; ++j)
        {
            if (vec[j] < vec[minPos])
                minPos = j;
        }

        if (minPos != i)
        {
            int tmp = vec[i];
            vec[i] = vec[minPos];
            vec[minPos] = tmp;
        }
    }
}

 

4.直接插入排序

为了实现N个数的排序，将后面N-1个数依次插入到前面已排好的子序列中，假定刚开始第1个数是一个已排好序的子序列，那么经过N-1趟就能得到一个有序序列。

void InsertSort(vector<int> &vec)
{
    int n = vec.size();
    int tmp, j;
    for (int i = 1; i < n; ++i)
    {
        tmp = vec[i];
        for (j = i - 1; j >= 0 && tmp < vec[j]; --j)
        {
            vec[j + 1] = vec[j];
        }
        vec[j + 1] = tmp;
    }
}

 

5.希尔排序

希尔排序(Shell Sort)是插入排序的一种，是对直接插入排序算法的改进该方法又称缩小增量排序。希尔排序通过比较相距一定间隔的元素，即形如L[i,i+d,i+2d,...i+kd]的序列然后缩小间距，再对各分组序列进行排序。直到只比较相邻元素的最后一趟排序为止，即最后的间距为1。

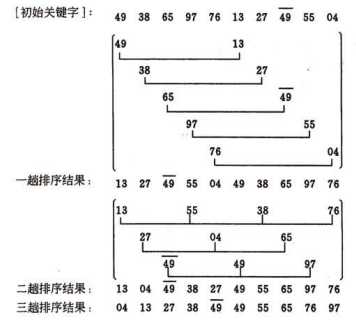
void ShellSort(vector<int> &vec)
{
    int n = vec.size();
    int i, j, tmp;
    int d = n / 2;//分成n/2组
    while (d >= 1)
    {
        //对每组进行直接插入排序
        for (int i = d; i < n; ++i)
        {
            tmp = vec[i];
            for (j = i - d; j >= 0 && tmp < vec[j]; j -= d)
            {
                vec[j + d] = vec[j];
            }
            vec[j + d] = tmp;
        }
        d /= 2;
    }
}

 

6.合并排序

合并排序采用分治法，思路是将两个或以上的有序表合并为一个有序表，把待排序的序列分割为若干个子序列，每个子序列有序，然后再把子序列合并为一个有序序列。若将两个有序表合并成一个有序表，则成为2路合并排序。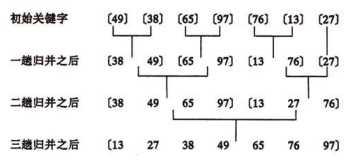

2-路归并就是将2个有序表组合成一个新的有序表。假定待排序表有n个元素，则可以看成是n个有序的子表，每个子表长度为1，然后两两归并...不停重复，直到合成一个长度为n的有序序列为止。Merge()函数是将前后相邻的两个有序表归并为一个有序表，设A[low...mid]和A[mid+1...high]存放在同一顺序表的相邻位置上，先将它们复制到辅助数组B中。每次从对应B中的两个段取出一个元素进行比较，将较小者放入A中。

//将两个有序序列vec[low..mid] vec[mid..high]合并
void Merge(vector<int> &vec, vector<int> &tmpArray, int low, int mid, int high)
{
    int i = low, j = mid + 1;
    int m = mid, n = high;
    int k = 0;
    while (i <= m && j <= n)
    {
        if (vec[i] <= vec[j])
            tmpArray[k++] = vec[i++];
        else
            tmpArray[k++] = vec[j++];
    }
    while (i <= m)
    {
        tmpArray[k++] = vec[i++];
    }
    while (j <= n)
    {
        tmpArray[k++] = vec[j++];
    }

    for (i = 0; i < k; ++i)
    {
        vec[low + i] = tmpArray[i];
    }
}

void MergeSort(vector<int> &vec, vector<int> &tmpArray, int low, int high)
{
    if (low < high)
    {
        int mid = low + (high - low) / 2;
        MergeSort(vec, tmpArray, low, mid);
        MergeSort(vec, tmpArray, mid + 1, high);
        Merge(vec, tmpArray, low, mid, high);
    }
}

void MergeSort(vector<int> &vec)
{
    int n = vec.size();
    vector<int> tmpArray(n);
    MergeSort(vec, tmpArray, 0, n - 1);
}

 

7.堆排序

堆排序是一种树形选择排序方法，在排序过程中，将L[n]看成是一棵完全二叉树的顺序存储结构，利用完全二叉树中双亲节点和孩子节点之间的内在关系，在当前无序区中选择关键字最大（或最小）的元素。堆排序的思路是：首先将序列L[n]的n个元素建成初始堆，由于堆本身的特点（以大根堆为例），堆顶元素就是最大值。输出堆顶元素后，通常将堆底元素送入堆顶，此时根结点已不满足大根堆的性质，堆被破坏，将堆顶元素向下调整使其继续保持大根堆的性质，再输出堆顶元素。如此重复，直到堆中仅剩下一个元素为止。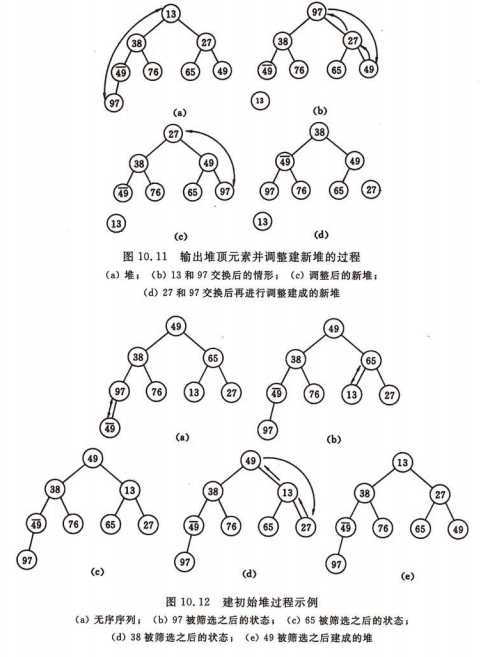

 

 

//使用数组二叉树 数组实现的堆中，第N个节点的左孩子的索引值是(2N+1)，右孩子的索引是(2N+2)
void HeapAdjust(vector<int> &vec, int root, int size)
{
    int child = 2 * root + 1;//左孩子
    if (child <= size - 1)//有左孩子
    {
        int rightChild = child + 1;
        if (rightChild <= size - 1)//有右孩子
            if (vec[child] < vec[rightChild])
                child = rightChild;
        if (vec[root] < vec[child])
        {
            int tmp = vec[child];
            vec[child] = vec[root];
            vec[root] = tmp;
            HeapAdjust(vec, child,size);
        }
    }
}

void HeapSort(vector<int> &vec)
{
    int size = vec.size();
    for (int i = size / 2 - 1; i >= 0; --i)
    {
        HeapAdjust(vec, i,size);
    }
    
    for (int i = size - 1; i > 0; --i)
    {
        int tmp = vec[0];
        vec[0] = vec[i];
        vec[i] = tmp;
        HeapAdjust(vec, 0, i);
    }    
}

 

8.桶排序

假设输入是由一个随机过程产生的[0, 1)区间上均匀分布的实数。将区间[0, 1)划分为n个大小相等的子区间（桶），每桶大小1/n：[0, 1/n)， [1/n, 2/n)， [2/n, 3/n)，…，[k/n, (k+1)/n )，…将n个输入元素分配到这些桶中，对桶中元素进行排序，然后依次连接桶输入0 ≤A[1..n] <1辅助数组B[0..n-1]是一指针数组，指向桶（链表）

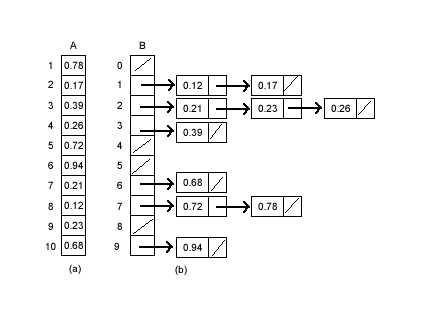
9.基数排序

基数排序可以说是桶排序的一种改进和推广，它不需要比较关键字的大小。它是根据关键字中各位的值，通过对排序的N个元素进行若干趟“分配”与“收集”来实现排序的。

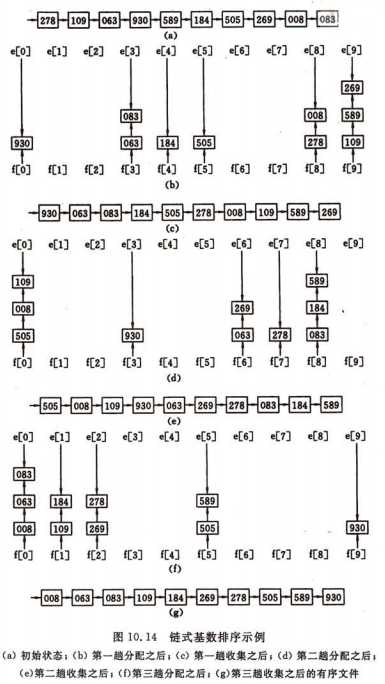
由于比较简单，这里就不给出代码了

 

10.计数排序

计数排序是一个类似于桶排序的排序算法，其优势是对已知数量范围的数组进行排序。它创建一个长度为这个数据范围的数组C，C中每个元素记录要排序数组中对应记录的出现个数。基本思想是对于给定的输入序列中的每一个元素x，确定该序列中值小于x的元素的个数。一旦有了这个信息，就可以将x直接存放到最终的输出序列的正确位置上。

计数排序很快，O(n)的时间复杂度，但是我们平时还是用的很少，是因为它需要一个至少等于待排序数组取值范围的缓冲区，而且通常只能用于正整数。

int Max(vector<int> &vec)
{
    if (vec.empty())
        return -1;
    int max = vec[0];
    for (auto num : vec)
    {
        if (max < num)
            max = num;
    }
    return max;
}

void CountSort(vector<int> &vec)
{
    int size = vec.size();
    int max = Max(vec);
    vector<int> countingArray(max+1);
    for (int i = 0; i < size; ++i)
    {
        countingArray[vec[i]]++;
    }

    int cur = 0, num = 0;
    while (cur < size)
    {
        while (countingArray[num] > 0)
        {
            vec[cur] = num;
            countingArray[num]--;
            cur++;
            if (cur >= size)
                break;
        }
        num++;
    }
}