计算子数组和最大（动态规划）

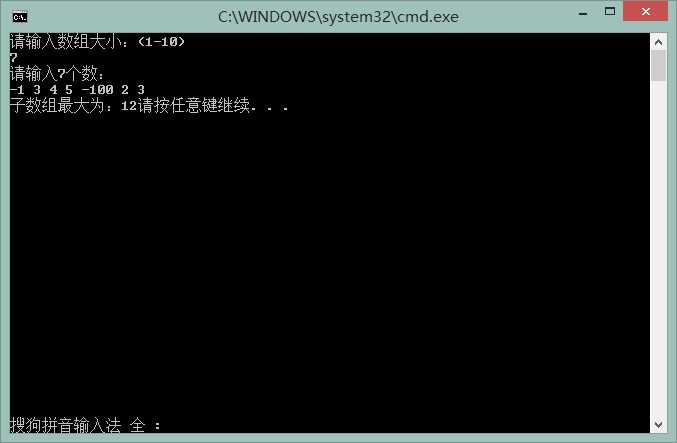
#include<iostream>
using namespace std;
#define N 100

int shuzu(int h,int array2[N])
{
    int i;
    int array3[N];
    array3[0]=array2[0];
    int maxsize=array3[0];
    for(i=1;i<=h;i++)
    {
        if(array3[i-1]>0)
        {
            array3[i]=array3[i-1]+array2[i];
            maxsize=max(maxsize,array3[i-1]);
        }
        else 
        {
            array3[i]=array2[i];

        }
    }
    cout<<"子数组最大为："<<maxsize;
    return 0;

}

int main()
{
    int i,j;
    cout<<"请输入数组大小：(1-10)"<<endl;
    cin>>j;

    int array1[N];

    cout<<"请输入"<<j<<"个数："<<endl;

    for(i=0;i<j;i++)
    {
        cin>>array1[i];
    }
    shuzu(j,array1);
    
    return 0;
}