排序算法总结

#include<stdio.h>
void main()
{
    int a[6]={2,1,5,3,6,7};
    int temp=0;
    int i=0;
    int j=0;
    int m=0;
    for(;i<6;i++)
        for(j=i;j<6-i;j++)
        {
            if(a[j+1]<a[j])
            {
                temp=a[j+1];
                a[j+1]=a[j];
                a[j]=temp;
            }
        }
    for(;m<6;m++)
    {
        printf("%d ",a[m]);
    }
}

#include<stdio.h>

void sort(int *a, int left, int right)
{
    int i = left;
    int j = right;
    int key = a[left];
    int m=0;
    
    if(left >= right)/*如果左边索引大于或者等于右边的索引就代表已经整理完成一个组了*/
    {
        for(m=0;m<6;m++)
            printf("%d ",a[m]);
        printf("\n");
        return ;
    }
    
     
    while(i < j)                               /*控制在当组内寻找一遍*/
    {
        while(i < j && key <= a[j])
        /*而寻找结束的条件就是，1，找到一个小于或者大于key的数（大于或小于取决于你想升
        序还是降序）2，没有符合条件1的，并且i与j的大小没有反转*/ 
        {
            j--;/*向前寻找*/
        }
         
        a[i] = a[j];
        /*找到一个这样的数后就把它赋给前面的被拿走的i的值（如果第一次循环且key是
        a[left]，那么就是给key）*/
         
        while(i < j && key >= a[i])
        /*这是i在当组内向前寻找，同上，不过注意与key的大小关系停止循环和上面相反，
        因为排序思想是把数往两边扔，所以左右两边的数大小与key的关系相反*/
        {
            i++;
        }
         
        a[j] = a[i];
    }
     
    a[i] = key;/*当在当组内找完一遍以后就把中间数key回归*/

    sort(a, left, i - 1);/*最后用同样的方式对分出来的左边的小组进行同上的做法*/
    sort(a, i + 1, right);/*用同样的方式对分出来的右边的小组进行同上的做法*/
                       /*当然最后可能会出现很多分左右，直到每一组的i = j 为止*/
}
void main()
{
    int a[6]={2,1,5,3,6,7};
    sort(a,0,5);
}

#include<stdio.h>
int main()
{
    int a[]={98,76,109,34,67,190,80,12,14,89,1};
    int k=sizeof(a)/sizeof(a[0]);
    int j;
    int i=1;
    int f=0;
    for(;i<k;i++)//循环从第2个元素开始
    {
        if(a[i]<a[i-1])
        {
            int temp=a[i];
            for(j=i-1;j>=0 && a[j]>temp;j--)//依次和前面的元素比较大小
            {
                a[j+1]=a[j];
            }
            a[j+1]=temp;//此处就是a[j+1]=temp;
        }
    return 0;
}

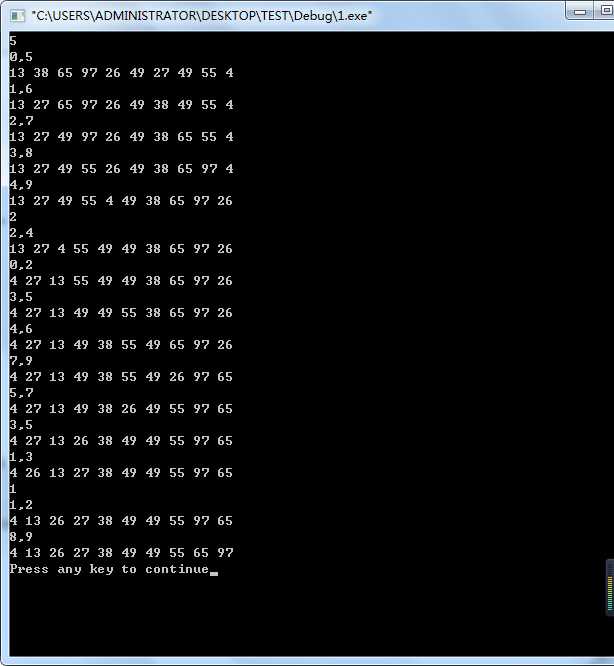
#include<stdio.h>
#include<math.h>
 
void shellsort3(int a[], int n)  
{  
       int i, j, gap;  
       int m=0;
       int temp=0;
      
        for (gap = n / 2; gap > 0; gap /= 2)  
        {
            printf("%d\n",gap);
            for (i = gap; i < n; i++)  
                for (j = i - gap; j >= 0 && a[j] > a[j + gap]; j -= gap)  
                {
                    temp=a[j];
                    a[j]=a[j+gap];
                    a[j+gap]=temp;
                    printf("%d,%d\n",j,j+gap);
                    for(m=0;m<10;m++)
                        printf("%d ",a[m]);
                    printf("\n");
                }
        }
}  
    
void main()
{
    int a[10] ={49,38,65,   97 ,  26,   13 ,  27,   49 ,  55 ,  4};
    shellsort3(a,10);
}

#include<stdio.h>
void SelectSort(int R[], int n)
{
  int i, j, m;
  int t;
  for(i=0; i<n-1; i++)
  {
    m = i;
    for(j = i+1; j < n; j++)
    {
        if(R[j] < R[m])
        m = j;
    }
    if(m != i)
    {
        t = R[i];
        R[i] = R[m];
        R[m] = t;
    }
  }
}
void main()
{
    int a[6]={2,1,5,3,6,7};
    int i=0;
    SelectSort(a,6);
    for(;i<6;i++)
        printf("%d ",a[i]);
}

#include <stdio.h>
//array是待调整的堆数组，i是待调整的数组元素的位置，nlength是数组的长度
//本函数功能是：根据数组array构建大根堆
void HeapAdjust(int array[],int i,int nLength)
{
    int nChild;
    int nTemp;
    for(;2*i+1<nLength;i=nChild)
    {
        //子结点的位置=2*（父结点位置）+1
        nChild=2*i+1;
        //得到子结点中较大的结点
        if(nChild<nLength-1&&array[nChild+1]>array[nChild])++nChild;
        //如果较大的子结点大于父结点那么把较大的子结点往上移动，替换它的父结点
        if(array[i]<array[nChild])
        {
            nTemp=array[i];
            array[i]=array[nChild];
            array[nChild]=nTemp; 
        }
        else break; //否则退出循环
    }
}
//堆排序算法
void HeapSort(int array[],int length)
{
    int i;
    //调整序列的前半部分元素，调整完之后第一个元素是序列的最大的元素
    //length/2-1是最后一个非叶节点，此处"/"为整除
    for(i=length/2-1;i>=0;--i)
    HeapAdjust(array,i,length);
    //从最后一个元素开始对序列进行调整，不断的缩小调整的范围直到第一个元素
    for(i=length-1;i>0;--i)
    {
        //把第一个元素和当前的最后一个元素交换，
        //保证当前的最后一个位置的元素都是在现在的这个序列之中最大的
        array[i]=array[0]^array[i];
        array[0]=array[0]^array[i];
        array[i]=array[0]^array[i];
        //不断缩小调整heap的范围，每一次调整完毕保证第一个元素是当前序列的最大值
        HeapAdjust(array,0,i);
    }
}
int main()
{
    int i;
    int num[]={9,8,7,6,5,4,3,2,1,0};
    HeapSort(num,sizeof(num)/sizeof(int));
    for(i=0;i<sizeof(num)/sizeof(int);i++)
    {
        printf("%d ",num[i]);
    }
    printf("\nok\n");
    return 0;
}