标签:
要求:
输入一个整形数组,数组里有正数也有负数。
数组中连续的一个或多个整数组成一个子数组,每个子数组都有一个和。
求所有子数组的和的最大值。要求时间复杂度为O(n)
发表一篇博客文章讲述设计思想,出现的问题,可能的解决方案(多选)、源代码、结果截图、总结。
设计思想:
首先利用动态数组node[NUM],将这个数组的长度输入,然后再输入数组中的每一个整数值。定义整型sum和max,将二者都初始化为node[0],sum用于存储子数组中前n项不为零的和,max用于存储最大值。利用for循环,每一次循环中,先判断sum是否小于0,是将node[ i ]的值赋给sum,否则sum=sum+node[ i ],然后判断max的值是否小于sum,是,执行max=sum。
出现的问题:
一开始看到题目,没有思绪,老师讲过一遍以后也是一头雾水,最后老师说用到的是“动态规划”的知识,上网搜也没有解决问题,最后花了一个多小时结合老师的讲解和网上的资料,勉强将这道题解决了。
可能的解决方案:
上网搜资料
源代码:

1 //chenchang 20143051 2016.4.5 2 //返回一个整数数组中最大子数组的和 3 #include<iostream> 4 using namespace std; 5 int main() 6 { 7 int NUM; 8 cout<<"Please input length of array:"; 9 cin>>NUM; 10 int *node=new int [NUM]; 11 for(int i=0;i<NUM;i++) 12 { 13 cout<<i+1<<" input:"; 14 cin>>node[i]; 15 } 16 ////////// 17 int sum=node[0]; 18 int max=node[0]; 19 for(int i=1;i<NUM;i++) 20 { 21 if(sum>0) 22 sum=node[i]+sum; 23 else 24 sum=node[i]; 25 if(max<sum) 26 max=sum; 27 } 28 cout<<"Max:"<<max<<endl; 29 delete [] node; 30 return 0; 31 }
结果截图:
图一:
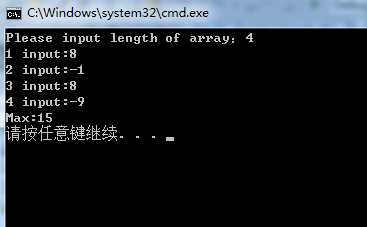
图二:
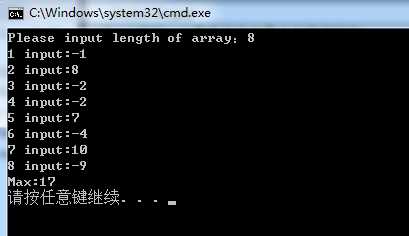
图三:
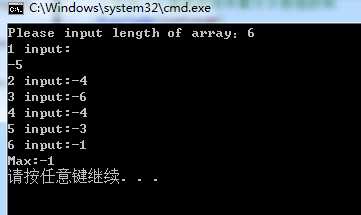
总结:
对于不会的知识点或没搞明白的知识点,可以上网搜索,网上有很多解释,参差不齐,一点要耐心查看。
标签:
原文地址:http://www.cnblogs.com/cchjl/p/5369709.html