聚类算法总结

标签：

K-measns Clustering

1)Original k-means clustering

最经典的聚类算法

init random k points 

until no change:

　　assign x to the cluster nearest

　　calculate mean for each cluster

　　replace mi for all clusters

缺点一个是k的选择，另一个是init是随机点，最后cluster的结果可能不同，需要测量多次。

2)Sequential k-means clustering

采用增量学习

make init guesses for m1...mk
set counts n1...nk=0
until interrupted:
    get next x
    if mi closest to x:
        ni++
        mi=mi+(1/ni)*(x-mi)

3)Forgetful sequential k-means clustering

增量越新的数据权重越大，随着数据增加，早期的数据影响就越小，表现时效性。a是0~1的constant

make init guesses m1...mk
until interrupted:
    get next x
    if mi closest to x:
        mi=mi+a*(x-mi)

可计算得m_n=(1-a)ⁿm₀+a∑(1-a)^n-kx_k  当n越大，m₀影响越小

Hierarchical clustering methods

分层聚合最终形成dendrogram

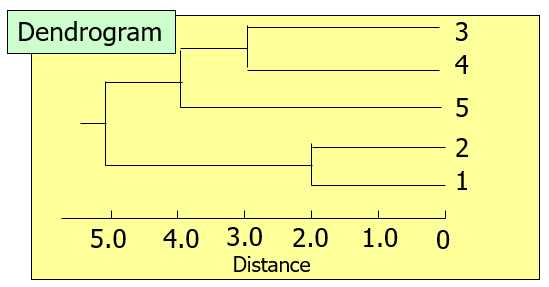
首先定义一下两个cluster的distance 

<1>single linkage

两个聚类中距离最短的对

<2>complete linkage

两个聚类中距离最长的对

<3>group average linkage

两个聚类中每一对点距离的平均

<4>centroid linkage

两个聚类中平均向量的距离- 会导致合并后的聚类偏向于大类

<5>median linkage

两个聚类中点距离

1)Agglomerative methods

从单个的元素不断聚合成一个整体

2)Division methods

从整体去分出各个类

例如有点 {1 2 3 4 5 6} ，先分成 1 vs 5 的两个聚类，有{1}{2,3,4,5,6} / {2}{1,3,4,5,6} .... 

计算每种分法的ditances，取最高的划分

然后计算剩下元素到两个聚类的距离，再分出一个到进新聚类中... 以此类推直到剩下的元素都靠近旧聚类。

· monothetic方法- 按照属性划分，通常用在binary variables

用CHI计算每个属性与其他属性集合的CHI值，独立性最大的划分出去。

Model-based clustering - EM algorithm

解决问题：传统方法每个x只能属于一类

使用高斯函数，计算x属于各个类的概率（权值）

每个类的Mean就使用xP(x)的均值

Density-based clustering - DBSCAN

解决问题：传统方法不能用于不规则形状聚类

ε-neighborhood of point p - N(p) ：与P距离为ε的集合

core points ：N(p)>=minpts

border points ：N(p)<minpts & N(p)包含core point

noise points ：非前面两种

①每个聚类至少有一个core

②core的N(p)中包含core，则两个core属于同个聚类

③border包含两个core，随机加入一个

④noise不属于任何聚类

Scalable clustering method - BIRCH

解决问题：不可扩展

L = {}
When there is a new data point x
    If L = {}
        Create cluster C containing x only
        Insert C into L
    Else
        Find the closest cluster C from x
        Insert x into C
        If C has diameter D greater than a given threshold, 
            Split cluster C into two sub-clusters C1 and C2
            Remove C from L
            Insert C1 and C2 into L
           

为了可扩展，记录clster feature(CF) =<n,LS,SS>

聚类算法总结

标签：

原文地址：http://www.cnblogs.com/IvanSSSS/p/5380860.html