标签:
题目:在一个二维数组的中,每一行都按照从左到右的递增顺序排列,每一列都按照从上到下的递增序列排序,请设计一个函数,输入这样的一个二维数组和一个整数,查询在此二维数组中是否存在此整数。
example:在下列数组中
1 2 8 9
2 4 9 12
4 7 10 13
6 8 11 15
查询是否有7存在,存在返回true,否则返回false(显然应该返回true)
查询是否有5存在,存在返回true,否则返回false(显然应该返回false)
这么简单?耿直的我立马就想到了暴力算法,一个一个比不就对了?
然而,然而要的是效率,如果这样解随便一个二维数组都可以这么做,显然忽略了已经给出来的条件:行递增,列也递增。
所以可以通过利用这个特征,在查找的过程中不停的排除一些数,不停的缩小查找规模从而找到比较好的解法。
故以查找7为例:
每次都把7和数组中右上角的数字比:
如果相等,那么即找到了此数字,直接返回true;
如果7小于此数字,而此数字又是本列中最小的数字,故去除此列,不再查找此列。
如果7大于此数字,而此数字又是本行中最大的数字,故去除此行,不再查找此行。
然后再把7和删除了行(或者列)的数组的右上角元素相比较;
如果删除了整个数组都没有找到,那么就返回false;未找到
7的整个具体查找过程如下图所示:(* 图片来自于《《剑指offer名气面试官精讲典型编程题》》作者:何海涛)
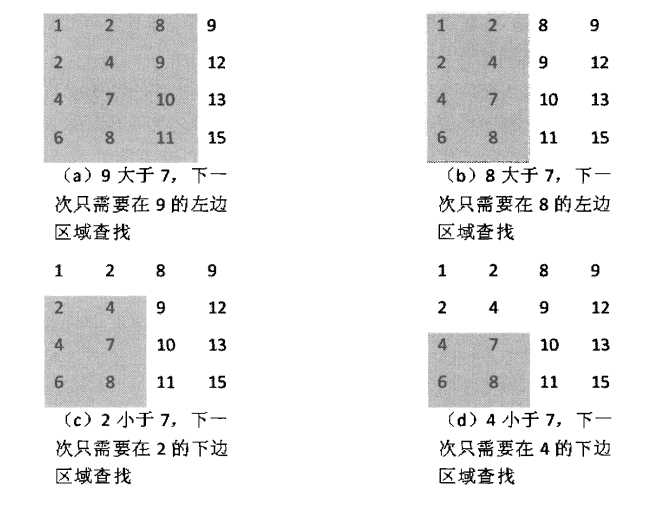
图中阴影部分为删除了行(或者列)之后剩下的查找范围,阴影部分变为空时还未找到那么就返回false。
故可以简单的写出如下代码:
1 #include<iostream> 2 using namespace std; 3 const int MaxSize = 4; 4 const int row = MaxSize;//行数 5 const int cols = MaxSize;//列数 6 /* 7 A:所要查找的数字 8 r:数组右上角数字的行号(初始为0) 9 c:数组右上角数字的列号(本例中初始为3) 10 */ 11 bool FindHaveA(int B[][MaxSize], int A, int r, int c) 12 { 13 if (r <= row-1&&c >= 0) //判断待查阴影区域是否为空 14 { 15 int mr = r, mc = c; 16 if (B[mr][mc] == A){ //相等返回true 17 //cout << "行号为:" << mr + 1 << "列号为:" << mc + 1 << endl; 18 return true; 19 } 20 else if (B[mr][mc] > A){ //>A 则去除此列 21 --mc; 22 } 23 else{ //<A 则去除此行 24 ++mr; 25 } 26 FindHaveA(B, A, mr, mc); //递归查找新的右上角元素 27 } 28 else 29 return false; //未找到 30 } 31 int main() 32 { 33 int B[][MaxSize] = { 1, 2, 8, 9, 2, 4, 9, 12, 4, 7, 10, 13, 6, 8, 11, 15 }; 34 bool R = FindHaveA(B, 7, 0, 3); //查7 35 //bool R = FindHaveA(B, 5, 0, 3); //查5 36 if (R) 37 cout << "true" << endl; 38 else 39 cout << "false" << endl; 40 system("pause"); 41 return 0; 42 }
标签:
原文地址:http://www.cnblogs.com/General-up/p/5392843.html