标签:
在平时的研究之余,希望每天晚上闲下来的时候,都学习一个机器学习算法,今天看到几篇不错的遗传算法的文章,在这里总结一下。
1 神经网络基本原理
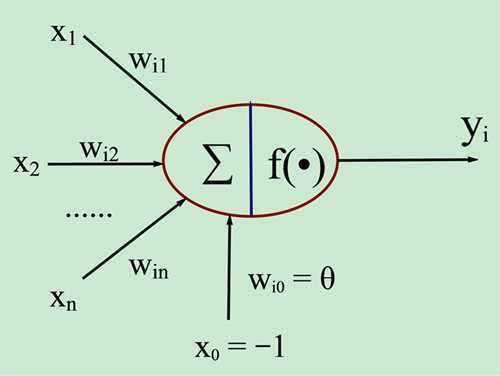
图1. 人工神经元模型
图中x1~xn是从其他神经元传来的输入信号,wij表示表示从神经元j到神经元i的连接权值,θ表示一个阈值 ( threshold ),或称为偏置( bias )。则神经元i的输出与输入的关系表示为:
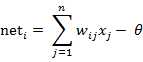
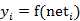
图中 yi表示神经元i的输出,函数f称为激活函数 ( Activation Function )或转移函数 ( Transfer Function ) ,net称为净激活(net activation)。若将阈值看成是神经元i的一个输入x0的权重wi0,则上面的式子可以简化为:
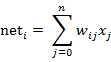
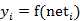
若用X表示输入向量,用W表示权重向量,即:
X = [ x0 , x1 , x2 , ....... , xn ]
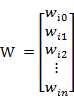
则神经元的输出可以表示为向量相乘的形式:
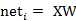
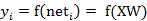
若神经元的净激活net为正,称该神经元处于激活状态或兴奋状态(fire),若净激活net为负,则称神经元处于抑制状态。
图1中的这种“阈值加权和”的神经元模型称为M-P模型 ( McCulloch-Pitts Model ),也称为神经网络的一个处理单元( PE, Processing Element )。
2. 常用激活函数
激活函数的选择是构建神经网络过程中的重要环节,下面简要介绍常用的激活函数。
(1) 线性函数 ( Liner Function )
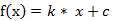
(2) 斜面函数 ( Ramp Function )
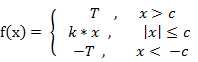
(3) 阈值函数 ( Threshold Function )
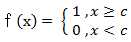
以上3个激活函数都属于线性函数,下面介绍两个常用的非线性激活函数。
(4) S形函数 ( Sigmoid Function )
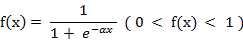
该函数的导函数:
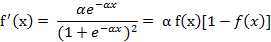
(5) 双极S形函数
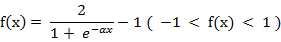
该函数的导函数:
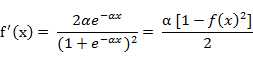
S形函数与双极S形函数的图像如下:
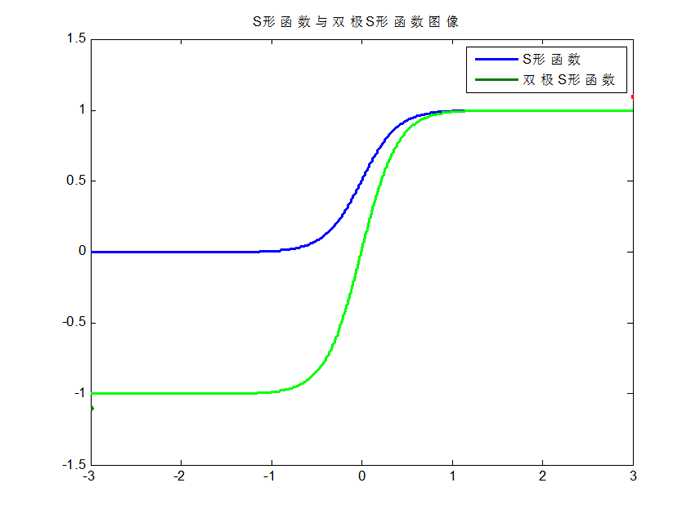
图3. S形函数与双极S形函数图像
双极S形函数与S形函数主要区别在于函数的值域,双极S形函数值域是(-1,1),而S形函数值域是(0,1)。
由于S形函数与双极S形函数都是可导的(导函数是连续函数),因此适合用在BP神经网络中。(BP算法要求激活函数可导)
3. 神经网络模型
神经网络是由大量的神经元互联而构成的网络。根据网络中神经元的互联方式,常见网络结构主要可以分为下面3类:
(1) 前馈神经网络 ( Feedforward Neural Networks )
前馈网络也称前向网络。这种网络只在训练过程会有反馈信号,而在分类过程中数据只能向前传送,直到到达输出层,层间没有向后的反馈信号,因此被称为前馈网络。感知机( perceptron)与BP神经网络就属于前馈网络。
图4 中是一个3层的前馈神经网络,其中第一层是输入单元,第二层称为隐含层,第三层称为输出层(输入单元不是神经元,因此图中有2层神经元)。
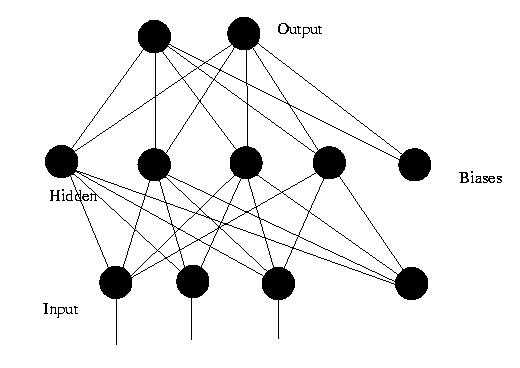
图4. 前馈神经网络
对于一个3层的前馈神经网络N,若用X表示网络的输入向量,W1~W3表示网络各层的连接权向量,F1~F3表示神经网络3层的激活函数。
那么神经网络的第一层神经元的输出为:
O1 = F1( XW1 )
第二层的输出为:
O2 = F2 ( F1( XW1 ) W2 )
输出层的输出为:
O3 = F3( F2 ( F1( XW1 ) W2 ) W3 )
若激活函数F1~F3都选用线性函数,那么神经网络的输出O3将是输入X的线性函数。因此,若要做高次函数的逼近就应该选用适当的非线性函数作为激活函数。
(2) 反馈神经网络 ( Feedback Neural Networks )
反馈型神经网络是一种从输出到输入具有反馈连接的神经网络,其结构比前馈网络要复杂得多。典型的反馈型神经网络有:Elman网络和Hopfield网络。
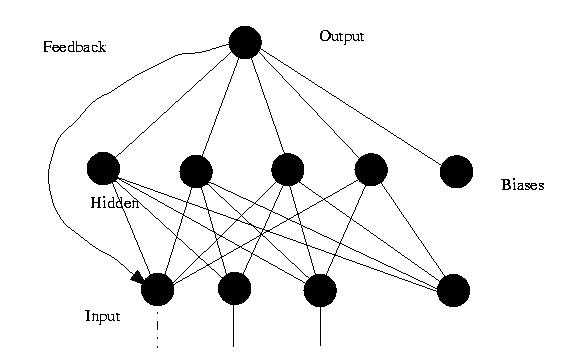
图5. 反馈神经网络
(3) 自组织网络 ( SOM ,Self-Organizing Neural Networks )
自组织神经网络是一种无导师学习网络。它通过自动寻找样本中的内在规律和本质属性,自组织、自适应地改变网络参数与结构。
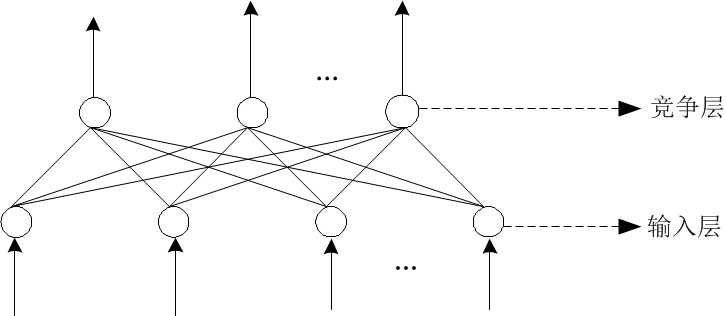
图6. 自组织网络
4. 神经网络工作方式
神经网络运作过程分为学习和工作两种状态。
(1)神经网络的学习状态
网络的学习主要是指使用学习算法来调整神经元间的联接权,使得网络输出更符合实际。学习算法分为有导师学习( Supervised Learning )与无导师学习( Unsupervised Learning )两类。
有导师学习算法将一组训练集 ( training set )送入网络,根据网络的实际输出与期望输出间的差别来调整连接权。有导师学习算法的主要步骤包括:
1) 从样本集合中取一个样本(Ai,Bi);
2) 计算网络的实际输出O;
3) 求D=Bi-O;
4) 根据D调整权矩阵W;
5) 对每个样本重复上述过程,直到对整个样本集来说,误差不超过规定范围。
BP算法就是一种出色的有导师学习算法。
无导师学习抽取样本集合中蕴含的统计特性,并以神经元之间的联接权的形式存于网络中。
Hebb学习律是一种经典的无导师学习算法。
(2) 神经网络的工作状态
神经元间的连接权不变,神经网络作为分类器、预测器等使用。
下面简要介绍一下Hebb学习率与Delta学习规则 。
(3) 无导师学习算法:Hebb学习率
Hebb算法核心思想是,当两个神经元同时处于激发状态时两者间的连接权会被加强,否则被减弱。
为了理解Hebb算法,有必要简单介绍一下条件反射实验。巴甫洛夫的条件反射实验:每次给狗喂食前都先响铃,时间一长,狗就会将铃声和食物联系起来。以后如果响铃但是不给食物,狗也会流口水。
受该实验的启发,Hebb的理论认为在同一时间被激发的神经元间的联系会被强 化。比如,铃声响时一个神经元被激发,在同一时间食物的出现会激发附近的另一个神经元,那么这两个神经元间的联系就会强化,从而记住这两个事物之间存在着 联系。相反,如果两个神经元总是不能同步激发,那么它们间的联系将会越来越弱。
Hebb学习律可表示为:
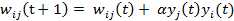
其中wij表示神经元j到神经元i的连接权,yi与yj为两个神经元的输出,a是表示学习速度的常数。若yi与yj同时被激活,即yi与yj同时为正,那么Wij将增大。若yi被激活,而yj处于抑制状态,即yi为正yj为负,那么Wij将变小。
(4) 有导师学习算法:Delta学习规则
Delta学习规则是一种简单的有导师学习算法,该算法根据神经元的实际输出与期望输出差别来调整连接权,其数学表示如下:
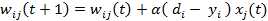
其中Wij表示神经元j到神经元i的连接权,di是神经元i的期望输出,yi是神经元i的实际输出,xj表示神经元j状态,若神经元j处于激活态则xj为 1,若处于抑制状态则xj为0或-1(根据激活函数而定)。a是表示学习速度的常数。假设xi为1,若di比yi大,那么Wij将增大,若di比yi小, 那么Wij将变小。
Delta规则简单讲来就是:若神经元实际输出比期望输出大,则减小所有输入为正的连接的权重,增大所有输入为负的连接的权重。反之,若神经元实际输出比 期望输出小,则增大所有输入为正的连接的权重,减小所有输入为负的连接的权重。这个增大或减小的幅度就根据上面的式子来计算。
(5)有导师学习算法:BP算法
采用BP学习算法的前馈型神经网络通常被称为BP网络。
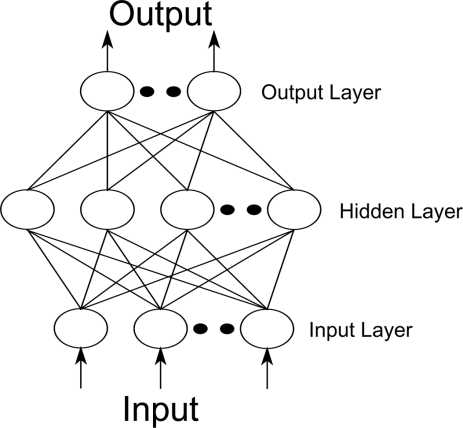
图8. 三层BP神经网络结构
BP网络具有很强的非线性映射能力,一个3层BP神经网络能够实现对任意非线性函数进行逼近(根据Kolrnogorov定理)。一个典型的3层BP神经网络模型如图7所示。
BP网络的学习算法占篇幅较大,我打算在下一篇文章中介绍。
5 实例
Hebb学习规则代表一种纯向前的非监督学习。这里用一个简单的例子来说明具有简单网络的二进制和连续激活函数的Hebb学习情况。如图:
学习常数在这里则设为 η = 1。因为初始权重具有非零值,这意味着这个网络事先已经明显受过训练。这里我们采用双机二进制神经元,
那么 f(net) = sgn(net)。
学习过程有以下步骤:
第一步 加到网络的输入X1产生如下的net1
net1 = (W1)TX1 = [1, -1, 0, 0.5]*[1, -2, 1.5, 0]T = 3
更新的权是
W2 = W1 + sgn(net1)X1 = W1 + X1 = [1, -1, 0, 0.5]T + [1, -2, 1.5, 0]T = [2, -3, 1.5, 0.5]T
其中在表达式右边的下标表示当前调节步数。
第二步 这次学习使用X2作输入,重复第一步的步骤 W3 = [1, -2.5, 3.5, 2]
第三步 这次学习使用X3作输入,重复第一步的步骤 W4 = [1, -3.5, 4.5, 0.5]
由上可见,具有离散f(net)和η = 1的学习分别产生加整个输入模式向量到权向量中或者从权中减去整个输入模式向量。在连续f(net)的情况,权增加/减少向量按比例缩小到输入模式的分数值。
下面看一个具有连续双极激活函数f(net),用输入X1和初始权W1的Hebb学习例子。
同在第一步概况那样,我们得到神经元输出值和对于 λ=1 更新权,和以前的情况比较,不同的是f(net), 现在的激活函数如下式f(net) = 2/[1+exp(-λ*net)] - 1
通过计算可得
f(net1) = 0.905 f(net2) = -0.077 f(net3) = -0.932
W2 = [1.905, -2.81, 1.357, 0.5]T W3 = [1.828, -2.772, 1.512, 0.616]T W4 = [1.828, -3.70, 2.44, -0.783]T
通过对比离散的和连续的激活函数,可见 对于连续的激活函数,权调节成锥形,但是一般是在同一方向上的。
文章来自 http://www.cnblogs.com/heaad/archive/2011/03/07/1976443.html
标签:
原文地址:http://www.cnblogs.com/rongyux/p/5392837.html