标签:
分治法的适?条件:
• 该问题的规模缩?到?定程度就可以容易地解决。
• 该问题可以分解为若?个规模较?的相同问题:递归思想的应?
• 该问题所分解出的各个?问题是相互独?的,即?问题之间不包含公共的?问题。
• 利?该问题分解出的?问题的解可以合并为该问题的解。
案例---快排:
(1)过程
• Divide (Partition)
– 对元素进?重排以得到这样?个划分
• 在某个位置s前?的所有元素都?于等于A[s]
• 在位置s后?的所有元素都?于等于A[s]
• Conquer: ?个划分确定后, A[s]的位置便确定,再对两个?数组递归地划分
• Combine: 原地排序in-place sort,?需合并
(2)算法分析
最好情况:所有划分均产?规模相等的两个?数组
Tbest(n) = 2Tbest(n/2) + O(n), (T(1) = 0)= O(nlogn)
最坏情况下:划分所产?的两个?数组分别包含n-1个元素和0个元素(待排序的数组已排好序!)
Tworst(n) = Tworst(n-1) + O(n),(T(1) = 0)= O(n2)
平均情况:假设划分可能在任意位置s出现的概率均为1/n,则平均“?较”时间T(n)的递归关系式为:
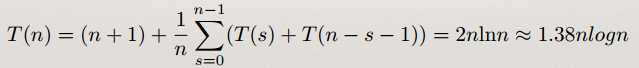
(3) 选择好的划分基准,产?好的划分:
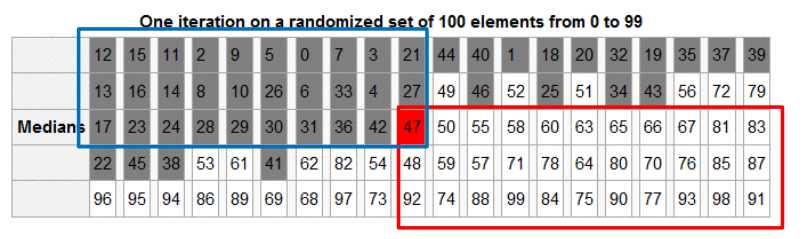
找到划分基准(近似中位数) : “中位数的中位数”
1. 将n个元素划分成?n/5?个组,每组5个元素(除了最后?组可能不是5个元素); O(1)
2. ?任意?种排序算法将每组中的5个元素排好序,并取出每组的中位数,共?n/5?个; O(n)
3. 递归找出这?n/5?个中位数的中位数,作为划分基准; T( ?n/5? )
• Divide
– 按近似中位数对输?数组进?Partition; O(n)
• Conquer
If k = s, return s // s为划分的位置
If p < k < s, 递归选择A[p…s-1]中第k?元素
If s < k < r, 递归选择A[s+1…r]中第k-(s-p+1)?元素
• Combine:?
棋盘覆盖:
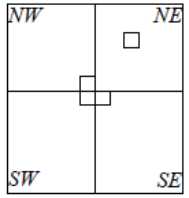
在?个2k×2k棋盘中,恰有?个?格与其他?格不同,称该?格为?特殊?格,且称该棋盘为?特殊棋盘。在棋盘覆盖问题中,要?图?的4种不同形态的L型?牌覆盖给定的特殊棋盘上除特殊?格以外的所有?格,且任何2个L型?牌不得重叠覆盖。
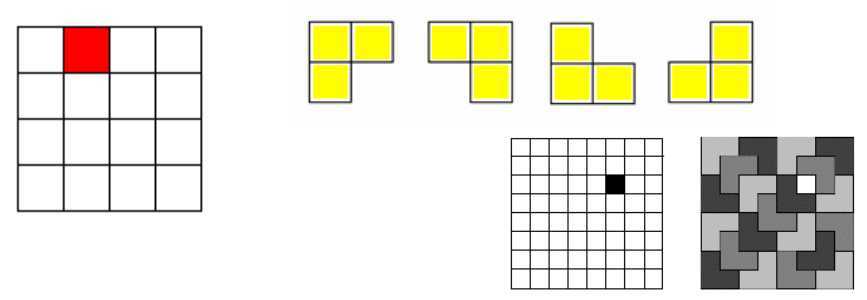
(1)该问题有解----数学归纳法
– 当n=1时( 2×2棋盘),该问题有解;
– 假设当n=k时( 2k×2k棋盘),该问题有解;
– 那么当n=k+1时( 2k+1×2k+1棋盘),将棋盘划分为4个
2k×2k?棋盘,特殊?格位于4个?棋盘之?中,?其余3个?棋盘中?特殊?格。
– 如何将这3个?特殊?格的?棋盘转化为特殊棋盘?
• ??个L型?牌覆盖这3个较?棋盘的会合处,将原问题转换为4个n=k时的?问题,因为n=k时有解,所以n=k+1时也有解。
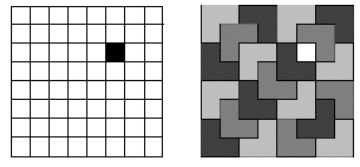
• 当k=0时( 1×1棋盘),即特殊?格,?牌数为0;
• 当k>0时,
- Divide:将2k×2k棋盘分割为4个2k-1×2k-1 ?棋盘。特殊?格位于4个较??棋盘之?中,?其余3个?棋盘中?特殊?格。
- 在递归之前要将原问题转化为4个较?规模的相同?问题。
- ??个L型?牌覆盖这3个?棋盘的会合处
- Conquer:递归地使?这种分割,直?棋盘缩?到1×1。
- Combine:?
标签:
原文地址:http://www.cnblogs.com/nolonely/p/5399360.html