标签:
Content
7 Machine Learning System Design
7.1 Prioritizing What to Work On
7.2 Error Analysis
7.3 Error Metrics for Skewed Classed
7.3.1 Precision/Recall
7.3.2 Trading off precision and recall: F1 Score
7.4 Data for machine learning
当我们着手针对某一实际问题设计机器学习系统时,我们应该在哪些方面花费较多的时间来使得系统的误差较少?以构建一个垃圾邮件分类器(a spam classifier)为例,我们可以从下面几个方面考虑:
很难说上述的哪一种方式最有效,而且每一种方式往往需要花费很多时间去研究调查。
解决机器学习问题的推荐做法是:
将误差转变为一个单一的数值非常重要,否则很难判断我们所是设计的学习算法的表现。
有时很难说误差的减少是否真正改善了算法。以癌症分类为例:
我们训练了一个logistic回归模型来预测病人是否得癌症 (y = 1 if cancer, y = 0 otherwise),我们在测试集上测得误差为1%(即正确诊断率99%)。但是,事实上病人患癌症的概率只有0.50%,也就是如果我们完全忽略特征量,直接令所有的y = 0,那么该模型的错误率只有0.5%。我们辛苦得到模型的误差居然比直接令y=0的误差大。这很让人生气! 但是仔细想想,直接令y = 0真的比我们训练出的模型好吗? 假设我们需要预测一个事实上已经患癌症(y=1)的病人,那么前者完全不可能预测正确,而后者却是有机会预测正确的。从这个角度看,我们训练得到的模型似乎更好。这也就说明了算法1比算法2的误差小,不一定算法1就好。
上述的情况通常发生在skewed classes的情况,即一类的数据远比另一类的数据多。对于这种情况,我们需要采取另一种方式来衡量一个学习算法的性能。
我们定义准确率(Precision)和召回率(Recall)如下所示,它们分别从两种角度衡量算法的性能。
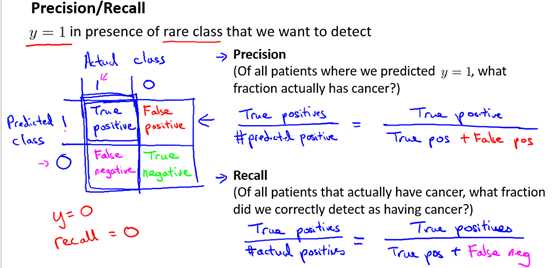
所以,当令y = 0时,Recall = 0 / (0 + #False neg) = 0, 即使它有很小的误差,但是它的召回率太低了。
注意,如果一个算法预测所有的情况都是negative,则Precision无定义,因为此时
#predicted positive = 0, 除0是无意义的。
在7.2节中我们提到,将误差转变为一个单一的数值非常重要,因为这样我们才能方便的比较不同算法之间的优劣。现在我们有precision和recall两个衡量标准,我们需要权衡两者。如果用Logistic回归模型预测病人是否患癌症,考虑下面的情况:
情况1: 假设考虑到一个正常人如果误判为癌症,将会承受不必要的心理和生理压力,所以我们要有很大把握才预测一个病人患癌症(y=1)。那么一种方式就是提高阙值(threshold),不妨设我们将阙值提高到0.7,即:
Predict 1 if: hθ(x)≥0.7
Predict 0 if: hθ(x)<0.7
在这种情况下,根据7.3.1节的定义,我们将会有较高的precision,但是recall将会变低。
情况2: 假设考虑到一个已经患癌症的病人如果误判为没有患癌症,那么病人可能将因不能及时治疗而失去宝贵生命,所以我们想要避免错过癌症患者的一种方式就是降低阙值,假设降低到0.3, 即
Predict 1 if: hθ(x)≥0.3
Predict 0 if: hθ(x)<0.3
在这种情况下,将得到较高的recall,但是precision将会下降。
情况1和情况2似乎是相互矛盾的,事实上,precision和recall往往是如下关系,并且高阙值对应高precision和低recall;低阙值对应低precision和高recall。
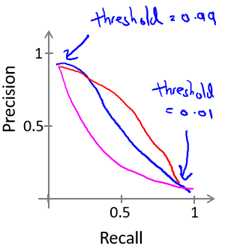
这样看来,我们不得不在precision和recall做出权衡。考虑下面的例子:
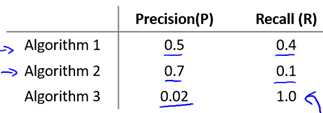
可以看出算法3是恒预测y=1(因为其recall = 1).
为了将precision(P)和recall(R)这两种度量方式转为一种单一的方式,一个简单的考虑是取二者的平均值,即: (P + R) / 2;但是这种方式似乎不太理想,因为如果这样,算法3将会被认为是最优的,而算法3是恒预测y=1,precision非常低。
事实上,一种更好的方式根据precision和recall的调和平均定义F1 Score如下:
1 / F1 = (1 / P + 1 / R) / 2
得 F1 = 2PR / (P + R)
要使F1较大,需要P和R同时较大,特别的,有:
注意:我们应该是在交叉检验集上测试F1的值,避免依赖测试集。
多少数据量对于我们训练学习算法是足够的呢?
通常来说,一个"劣等"算法(inferior algorithm),如果给它足够的数据来学习,它的表现往往优于一个缺乏数据学习的"优等"算法(superior algorithm)。所以在机器学习界有一个这样的共识:
"It‘s not who has the best algorithm that wins. It‘s who has the most data."
(我想这就是BIG DATA的魅力吧)
值得注意的是,为了充分利用数据,我们应该选择包含足够信息的特征量。通常一个判断参考是,给出输入x,一个人类的专家是否能够自信的预测出y。
数据量大能够起作用的基本原理是,可以使用一个具有大量参数的学习算法(e.g. logistic regression/linear regression with many features; neural network with many hidden units)来保证偏差较小,然后使用大量的训练集来大大减弱过拟合(方差较小),从而达到训练出一个在测试集上误差较小的,泛化能力强的模型。
Stanford机器学习笔记-7. Machine Learning System Design
标签:
原文地址:http://www.cnblogs.com/llhthinker/p/5402870.html