机器学习笔记—EM 算法

标签：

EM 算法所面对的问题跟之前的不一样，要复杂一些。

EM 算法所用的概率模型，既含有观测变量，又含有隐变量。如果概率模型的变量都是观测变量，那么给定数据，可以直接用极大似然估计法，或贝叶斯估计法来估计模型参数，但是，当模型含有隐变量时，情况就复杂一些，相当于一个双层的概率模型，要估计出两层的模型参数，就需要换种方法求解。EM 算法是通过迭代的方法求解。

监督学习是由训练数据 {(x⁽¹⁾,y⁽¹⁾),(x⁽²⁾,y⁽²⁾),...,(x^(m),y^(m))} 学习条件概率分布 P(Y|X) 或决策函数 Y=f(X) 作为模型，用于分类、回归等任务，这时训练数据中的每个样本点由输入和输出组成。但有时训练数据只有输入没有对应的输出 {(x⁽¹⁾,•),(x⁽²⁾,•),...,(x^(m),•)}，从这样的数据学习模型称为非监督学习问题。EM 算法可用于生成模型的非监督学习，生成模型由联合概率分布 P(X,Y) 表示，可以认为非监督学习训练数据是联合概率分布产生的数据。X 为观测数据，Y 为未观测数据。

我们先不管上一篇文章介绍的高斯混合模型，先来看通用的 EM 算法。

假设有训练集 {x⁽¹⁾,x⁽²⁾,...,x^(m)}，我们要寻找模型 p(x,z) 的参数来拟合这些数据，数据的似然估计为：

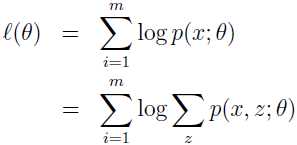
要直接使用极大似然估计来求 θ 是很难的，因为 z⁽ⁱ⁾ 是隐随机变量，如果 z⁽ⁱ⁾ 不是隐变量，而是可以观察到的，那使用极大似然估计就简单多了。

在这种情况下，EM 算法给出了一种高效的极大似然估计方法，直接最大化 L(θ) 很难，我们的策略是不断地构建 L 的下界（E-step），然后优化下界（M-step）。

对于每个 i，使 Q_i 为 z 上的分布（∑_zQ_i(z)=1，Q_i(z)≥0），那么

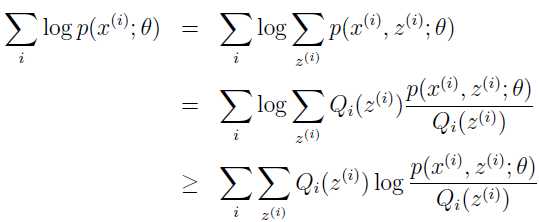
最后一步的推导是用了 Jensen 不等式定理和 f(x)=log(x) 是凹函数的事实。

本文我们介绍 EM 算法的一个重要应用，高斯混合模型的参数估计。高斯混合模型应用广泛，在许多情况下，EM 算法是学习高斯混合模型的有效方法。

假设有训练集 {x⁽¹⁾,x⁽²⁾,...,x^(m)}，要把数据建模成一个联合分布 p(x⁽ⁱ⁾,z⁽ⁱ⁾)=p(x⁽ⁱ⁾|z⁽ⁱ⁾)p(z⁽ⁱ⁾)，其中 z⁽ⁱ⁾~Multinomial(Φ)，x⁽ⁱ⁾|z⁽ⁱ⁾=j~N(µ_j,∑_j)，k 表示 z⁽ⁱ⁾ 的可取值个数。数据 x⁽ⁱ⁾ 是这样生成的：先从 {1,...,k} 中随机选择一个 z⁽ⁱ⁾，再从 z⁽ⁱ⁾ 所关联的高斯分布中生成 x⁽ⁱ⁾。这就是高斯混合模型，其中 z⁽ⁱ⁾ 是隐变量，也就是未观测变量，正是这个变量使得问题变得复杂。

这个模型的参数是 Φ，μ 和 ∑，我们的任务就是估计出这些参数。

参考资料：

[1] http://cs229.stanford.edu/notes/cs229-notes8.pdf

[2] 李航,著.统计学习方法[M]. 清华大学出版社, 2012

机器学习笔记—EM 算法

标签：

原文地址：http://www.cnblogs.com/NaughtyBaby/p/5405576.html