标签：
Sparse AutoEncoder是一个三层结构的网络，分别为输入输出与隐层，前边自编码器的描述可知，神经网络中的神经元都采用相同的激励函数，Linear Decoders 修改了自编码器的定义，对输出层与隐层采用了不用的激励函数，所以 Linear Decoder 得到的模型更容易应用，而且对模型的参数变化有更高的鲁棒性。
在网络中的前向传导过程中的公式：
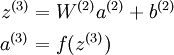
其中 a(3) 是输出. 在自编码器中, a(3) 近似重构了输入 x = a(1) 。
对于最后一层为 sigmod(tanh) 激活函数的 autoencoder ，会直接将数据归一化到 [0,1] ，所以当 f(z(3)) 采用 sigmod(tanh) 函数时，就要对输入限制或缩放，使其位于 [0,1] 范围中。但是对于输入数据 x ，比如 MNIST，但是很难满足 x 也在 [0,1] 的要求。比如， PCA 白化处理的输入并不满足 [0,1] 范围要求。
另 a(3) = z(3) 可以很简单的解决上述问题。即在输出端使用恒等函数 f(z) = z 作为激励函数，于是有 a(3) = f(z(3)) = z(3)。该特殊的激励函数叫做 线性激励 (恒等激励)函数。
Linear Decoder 中隐含层的神经元依然使用 sigmod（tanh）激励函数。隐含单元的激励公式为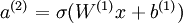 
,其中 
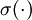是 S 型函数, x 是入, W(1) 和 b(1) 分别是隐单元的权重和偏差项。即仅在输出层中使用线性激励函数。这用一个 S 型或 tanh 隐含层以及线性输出层构成的自编码器，叫做线性解码器。
在线性解码器中，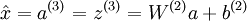
。因为输出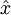 
是隐单元激励输出的线性函数，改变 W(2) ，即可使输出值 a(3) 大于 1 或者小于 0。这样就可以避免在 sigmod 对输出层的值缩放到 [0,1] 。
随着输出单元的激励函数的改变，输出单元的梯度也相应变化。之前每一个输出单元误差项定义为：
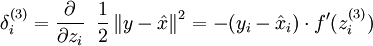
其中 y = x 是所期望的输出, 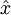是自编码器的输出, 
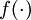是激励函数.因为在输出层激励函数为 f(z) = z, 这样 f‘(z) = 1，所以上述公式可以简化为
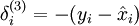
当然，若使用反向传播算法来计算隐含层的误差项时:
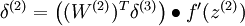
因为隐含层采用一个 S 型（或 tanh）的激励函数 f,在上述公式中，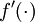
依然是 S 型（或 tanh）函数的导数。即Linear Decoder中只有输出层残差是不同于autoencoder 的。
Liner Decoder 代码：
（六）6.16 Neurons Networks linear decoders and its implements
标签：
原文地址：http://www.cnblogs.com/ooon/p/5407117.html
