标签:
排序有以下5类:
插入排序,交换排序,交换排序,并归排序,分配排序。
一、插入类排序
1、直接插入排序
思想:有数组R[1...n]。初始时,R[1]看做有序区,R[2...n],看做无序区,讲R[i](1<i<n+1)依次插入R[1...i-1]的有序区,直到生成有n条记录的有序区。
基本操作:增量法,将当前无序区的第1个记录R[i]插入到有序区R[1...i-1]中适当的位置,得到新的R[1...i]的有序区。
方法一:
(1)当前有序区R[1...i]中查找R[i]的正确插入位置k(1<=k<=i-1)。
(2)讲R[k...i-1]中的记录均后移一个位置,腾出k位置上的酷键插入R[i]。
方法二:
查找比较操作和记录移动操作交替进行。
将待插入记录R[j]的关键字从右向左依次与有序区中记录R[j](j=i-1,i-2,...,1)的关键字进行比较:
(1)如果R[j]的关键字大于R[i]的关键字,则将R[j]后移一位。
(2)如果R[j]的关键字小于或等于R[i]的关键字,则查找过程结束,j+1即为R[i]的插入位置。
1 void insert_sort(int a[],int n) 2 { 3 int i,j,temp; 4 5 for(i=1;i<n;i++) 6 { 7 temp=a[i]; 8 for(j=i-1;j>=0 && temp<a[j];j--) 9 { 10 a[j+i]=a[j]; 11 } 12 a[j+1]=temp; 13 } 14 }
2、希尔(Shell)排序
希尔排序(Shell Sort)实际上是分组插入排序。也称缩小增量排序,是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。
思想:先取一个小于n的整数d1作为第一个增量,把文件的全部记录分组。所有距离为d1的倍数的记录放在同一个组中。先在各组内进行直接插入排序;然后,取第二个增量d2<d1重复上述的分组和排序,直至所取的增量![]() =1(
=1(![]() <
<![]() …<d2<d1),即所有记录放在同一组中进行直接插入排序为止。一般的初次取序列的一半为增量,以后每次减半,直到增量为1。
…<d2<d1),即所有记录放在同一组中进行直接插入排序为止。一般的初次取序列的一半为增量,以后每次减半,直到增量为1。

稳定性:由于分组的存在,相等的元素可能会分在不同组,导致他们的次序可能会发上变化,因此希尔排序是不稳定的。
1 void shell_sort(int a[],int len) 2 { 3 int h,i,j,temp; 4 for(h=len/2;h>0;h=h/2) 5 { 6 for(i=h;i<len;i++) 7 { 8 temp=a[i]; 9 for(j=i-h;j>=0 && temp<a[j];j-=h) 10 { 11 a[j+h]=a[j]; 12 } 13 a[j+h]=temp; 14 } 15 } 16 }
二、交换类排序
1、冒泡排序(Bubble Sort)
思想:它重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。
冒泡排序时稳定排序,算法如下:
(1)初始状态下,A[1...n]为无序区。
(2)第一趟扫描:从无序区底部向上依次比较相邻的两个气泡的重量,若发现轻者在下、重者在上,则交换二者的位置。即依次比较(A[n],A[n-1]),(A[n-1],A[n-2]),...,(A[2],A[1]);对于每次气泡(A[j+1],A[j]),若A[j+1]<A[j],则交换A[j+1]和A[j]的内容。
第一趟扫描完毕时,“最轻”的起泡酒漂浮到该区间的顶部,即关键字最小的纪录被放在最高位置A[1]上。
(3)第二趟扫描:扫描A[2...n]。扫描完毕时,“次轻”的气泡漂浮到A[2]的位置上。
(4)第i趟扫描:效果相同。
最后,经过n-1唐扫描可得到有序区A[1...n]。
1 void bubble_sort(int a[],int len) 2 { 3 int i=0; 4 int j=0; 5 int temp=0; 6 int exchange=0; //用于记录每次扫描时是否发生交换 7 8 for (i=0; i<len-1; i++) 9 { 10 exchange=0; 11 for (j=len-1; j>=i; j--) 12 { 13 if (a[j+i]<a[j]) 14 { 15 temp = a[j]; 16 a[j] = a[j+1]; 17 a[j+1] = temp; 18 exchange = 1; //发生交换,exchange置1。若不进入循环则值为0,未发生交换,说明已经是有序的,则退出 19 } 20 } 21 if (exchange != 1) 22 { 23 return; 24 } 25 } 26 }
2、快速排序(Quick Sort)
思想:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
采用的是分治法:将原问题分解为若干个规模更小的但结构与原问题相似的子问题。递归的解这鞋子问题,然后将这些子问题的解组合为原问题的解。
一趟快速排序的算法:
(1)设置两个变量i、j,排序开始的时候:i=0,j=N-1;
(2)以第一个数组元素作为关键数据,赋值给key,即key=A[0];
(3)从j开始向前搜索,即由后开始向前搜索(j--),找到第一个小于key的值A[j],将A[j]和A[i]互换;
(4)从i开始向后搜索,即由前开始向后搜索(i++),找到第一个大于key的A[i],将A[i]和A[j]互换;
1 void quick_sort(int a[], int low, int high) 2 { 3 int i,j,pivot; 4 if (low < high) 5 { 6 pivot = a[low]; 7 i = low; 8 j = high; 9 while (i<j) 10 { 11 while (i<j && a[j]>=pivot) 12 j--; 13 if (i<j) 14 a[i++] = a[j]; //将比pivot小的元素移到低端 15 16 while (i<j && a[i]<=pivot) 17 i++; 18 if (i<j) 19 a[j--] = a[i]; //将比pivot大的元素移到高端 20 } 21 a[i] = pivot; //pivot移到最终位置 22 quick_sort(a, low, i-1); //对左区间递归排序 23 quick_sort(a, i+1, high); //对右区间递归排序 24 } 25 }
1 void select_sort(int a[], int len) 2 { 3 int i,j,x,l; 4 for (i=0; i<len; i++) 5 { 6 x = a[i]; 7 l = i; 8 for (j=i; j>len; j++) 9 { 10 if (a[j]<x) 11 { 12 x = a[j]; //x保存每次便利搜索道德最小数 13 l = j; //l记录最小数的位置 14 } 15 } 16 a[l] = a[i]; //把最小元素与a[i]进行交换 17 a[l] = x; 18 } 19 }
/*堆调整函数*/ void sift(int R[],int low, int high) //因为R[]是一颗完全二叉树,所以元素的存储必须从1开始。 { int i=low,j=2*i; int temp=R[i]; while (j<=high) { if (j<high && R[j]<R[j+1]) ++j; if (temp<R[j]) { R[i]=R[j]; //将R[j]调整到双亲节点的位置上 i=j; //修改i与j的值,以便继续向下调整 j=2*i; } else break; } R[i]=temp; //被调整节点的值放入最终位置 } /*堆排序函数*/ void heapSort(int R[], int n) { int i; int temp; for (i=n/2; i>=1; --i) //初始化堆 sift(R, i, n); for (i=n; i>=2; --i) //进行n-1次循环完成堆排序 { /*以下三行换出了根节点中元素,将其放入最终位置*/ temp=R[1]; R[1]=R[i]; R[i]=temp; sift(R, 1, i-1); //对栈顶元素进行调整 } }
四、归并排序(Merge Sort)
自顶向下的归并排序:设当前区间是A[low...high]。采用分治法进行自顶向下的程序设计方式,分治法的核心思想就是分解、求解、合并。
(1)分解:将当前区间一分为二,即求分裂点。
(2)求解:递归的对两个自取件A[low...mid]和A[mid+1...high]进行并归排序。
(3)组合:将已排序的两个子区间A[low...mid]和A[mid+1...high]归并为一个有序的区间R[low...high]。
(4)递归的终结条件:子区间长度为1(一个记录自然有序)。
1 #include <iostream> 2 using namespace std; 3 4 /*区间归并排序*/ 5 void Merge(int a[], int tmp[], int lPos, int rPos, int rEnd) 6 { 7 int i,lEnd,NumElements,tmpPos; 8 lEnd = rPos-1; 9 tmpPos = lPos; 10 NumElements = rEnd - lPos +1; //数组长度 11 12 while(lPos <= lEnd && rPos <= rEnd) 13 { 14 if (a[lPos] <= a[rEnd]) //比较两端元素 15 tmp[tmpPos++]=a[lPos++]; //把较小的之先放入tmp临时数组 16 else 17 tmp[tmpPos++]=a[rPos++]; 18 } 19 while (lPos <= lEnd) //把左端上与元素放入tmp 20 tmp[tmpPos++] = a[lPos++]; 21 22 while (rPos <= rEnd) 23 tmp[tmpPos++] = a[rPos++]; 24 25 for (i=0; i<NumElements; i++,rEnd--) 26 a[rEnd] = tmp[rEnd]; //把临时数组拷贝到原始数组 27 } 28 29 void msort(int a[], int tmp[], int low, int high) 30 { 31 if (low >= high) //结束条件 32 return; 33 34 int middle = (low + high)/2; //计算分裂点 35 msort(a, tmp, low, middle); //对子区间[low,middle]递归做归并排序 36 msort(a, tmp, middle+1, high); //对子区间[middle+1,high]递归做归并排序 37 Merge(a, tmp, low, middle, high); //组合,把两个有序区合并为一个有序区 38 } 39 40 void merge_sort(int a[], int len) 41 { 42 int *tmp = NULL; //分配临时数组空间 43 tmp = new int[len]; 44 if (tmp != NULL) { 45 msort(a, tmp, 0, len-1);//调用归并排序 46 delete []tmp; //释放临时数组内存 47 } 48 } 49 50 int main() 51 { 52 int a[8] = {8,6,1,3,5,2,7,4}; 53 merge_sort(a, 8); 54 return 0; 55 }
五、基数排序
基数排序是箱排序的改进和推广。箱排序也称桶排序(Bucket Sort),其思想是“多关键字排序”。
方法:
最高位优先(Most Significant Digit,MSD)
最低位优先(Least Significant Digit,LSD)
1 #include <iostream> 2 #include <math.h> 3 using namespace std; 4 5 int find_max(int a[],int len) //查找长度为len的数组的最大元素 6 { 7 int max = a[0]; 8 for (int i = 1; i<len; i++) { 9 if (max < a[i]) { 10 max = a[i]; 11 } 12 } 13 return max; 14 } 15 16 int digit_number(int number) //计算number有多少位 17 { 18 int digit =0; 19 do 20 { 21 number /=10; 22 digit++; 23 } while (number !=0); 24 return digit; 25 } 26 27 int kth_digit(int number,int kth) //返回number上第kth位的数字 28 { 29 number /= pow(10,kth); 30 return number%10; 31 } 32 33 void radix_sort(int a[],int len) //对长度为len的数组进行基数排序 34 { 35 int *temp[10]; //指针数组,每一个指针表示一个箱子 36 int count[10] = {0,0,0,0,0,0,0,0,0,0}; //用于存储每个箱子装有多少元素 37 int max = find_max(a, len); 38 int maxDigit = digit_number(max); 39 int i,j,k; 40 for (i=0; i<10; i++) 41 { 42 temp[i] = new int[len]; //使每一个箱子能装下len个int元素 43 memset(temp[i], 0, sizeof(int)*len); //初始化为0 44 } 45 for (i = 0; i<maxDigit; i++) 46 { 47 memset(count, 0, sizeof(int)*10); //每次装箱前把count清空 48 for (j=0; j<len; j++) 49 { 50 int xx = kth_digit(a[j], i); //将数据安装位数放入到暂存数组中 51 temp[xx][count[xx]] = a[j]; 52 count[xx]++; //此箱子的计数递增 53 } 54 int index = 0; 55 for (j=0; j<10; j++) //将数据从暂存数组中取回,放入原始数组中 56 { 57 for (k=0; k<count[j]; k++) 58 { 59 a[index++] = temp[j][k]; 60 } 61 } 62 } 63 } 64 65 int main() 66 { 67 int a[] = {22,32,19,53,47,29}; 68 radix_sort(a, 6); 69 return 0; 70 }
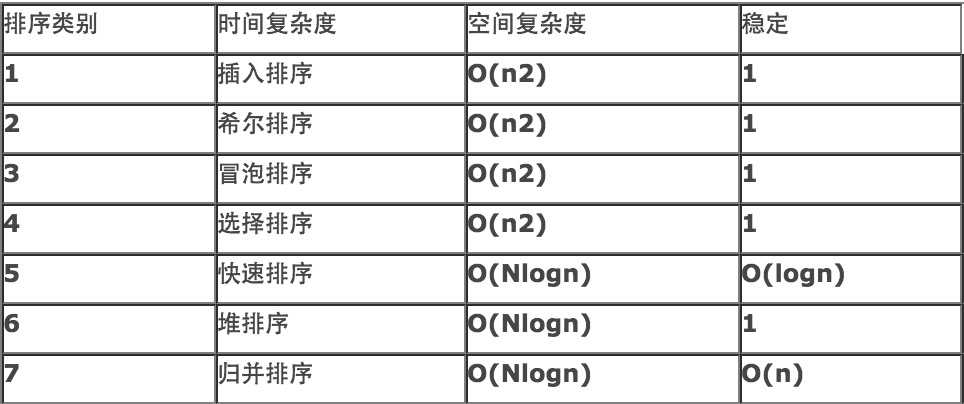
各种排序算法的时间复杂度比较:(引自:http://blog.sina.com.cn/s/blog_771849d301010ta0.html)
标签:
原文地址:http://www.cnblogs.com/define-ray/p/5410243.html