标签:
后缀数组(Suffix Array,SA)是处理字符串的有力工具。它比后缀树更易实现,占用空间更少,并且同样可以解决千变万化的字符串问题
首先推荐罗穗骞的论文(网上搜一下就能搜到),里面对后缀数组的定义、实现和应用都做了详细的阐述
然而不幸的是罗神犇的代码简直魔性,蒟蒻表示这代码压的根本看不懂啊……
所以在理解了后缀数组的构建过程之后,我重新写了一份模板代码。虽然啰嗦了点(代码比较大,而且变量名故意拉长了),不过相对比较好懂
而且论文中用到的辅助空间是4N,我的模板用了3N,事实上还可以优化到只需2N。空间优化的核心思想就是:当SA和rank数组“闲置”时,它们就是辅助数组
(如果字符集很大,那么辅助空间就会是4N(优化后为3N))
Template:

1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 5 const int maxN=200005; 6 7 int suffixArray[maxN]; //1-based 8 int suffixRank[maxN]; //1-based 9 int height[maxN]; //LCP length of SA[i] and SA[i-1] 10 11 char objStr[maxN]; 12 int objCoded[maxN]; //begin with objCoded[1] 13 int objLen; 14 15 inline int codeChar(char x) 16 { 17 return x+1-‘a‘; 18 } //range:[1..26] 19 20 void input() 21 { 22 scanf("%d",&objLen); 23 for(int i=0;i<objLen;i+=80) scanf("%s",objStr+i); 24 25 for(int i=1;i<=objLen;i++) 26 objCoded[i]=codeChar(objStr[i-1]); 27 objCoded[objLen+1]=-1; 28 } 29 30 const int alphabetSize=26; 31 32 int charCount[alphabetSize+1]; 33 34 int secondKey[maxN]; //use suffixArray[] itself as firstKey 35 int radixCount[maxN]; 36 int suffixTemp[maxN]; 37 38 void buildSuffixArray() 39 { 40 memset(charCount,0,sizeof(charCount)); 41 42 for(int i=1;i<=objLen;i++) 43 ++charCount[objCoded[i]]; 44 45 for(int i=2;i<=alphabetSize;i++) 46 charCount[i]+=charCount[i-1]; 47 48 for(int i=1;i<=objLen;i++) 49 suffixRank[i]=charCount[objCoded[i]]; 50 51 for(int step=1;step<objLen;step<<=1) 52 { 53 for(int i=1;i<=objLen;i++) 54 secondKey[i]=(i+step<=objLen)?suffixRank[i+step]:0; 55 56 memset(radixCount,0,sizeof(radixCount)); 57 58 for(int i=1;i<=objLen;i++) 59 ++radixCount[secondKey[i]]; 60 61 for(int i=1;i<=objLen;i++) 62 radixCount[i]+=radixCount[i-1]; 63 64 for(int i=objLen;i;i--) 65 { 66 int pos=radixCount[secondKey[i]]--; 67 suffixTemp[pos]=i; 68 } 69 70 memset(radixCount,0,sizeof(radixCount)); 71 72 for(int i=1;i<=objLen;i++) 73 ++radixCount[suffixRank[i]]; 74 75 for(int i=1;i<=objLen;i++) 76 radixCount[i]+=radixCount[i-1]; 77 78 for(int i=objLen;i;i--) 79 { 80 int& cur=suffixTemp[i]; 81 int pos=radixCount[suffixRank[cur]]--; 82 suffixArray[pos]=cur; 83 } 84 85 int last=suffixRank[suffixArray[1]]; 86 suffixRank[suffixArray[1]]=1; 87 bool finished=true; 88 89 for(int i=2;i<=objLen;i++) 90 { 91 int& curPos=suffixArray[i]; 92 int& lastPos=suffixArray[i-1]; 93 int temp=suffixRank[curPos]; 94 if(temp==last && secondKey[curPos]==secondKey[lastPos]) 95 { 96 suffixRank[curPos]=suffixRank[lastPos]; 97 finished=false; 98 } 99 else 100 suffixRank[curPos]=i; 101 last=temp; 102 } 103 104 if(finished) break; 105 } 106 } 107 108 void buildHeight() 109 { 110 memset(height,0,sizeof(height)); 111 112 for(int i=1;i<=objLen;i++) 113 { 114 int& curRank=suffixRank[i]; 115 int& lastRank=suffixRank[i-1]; 116 if(curRank>1) 117 { 118 height[curRank]=height[lastRank]?height[lastRank]-1:0; 119 int& lastSA=suffixArray[curRank-1]; 120 int& curSA=suffixArray[curRank]; //curSA=i 121 for(;;height[curRank]++) 122 { 123 if(objCoded[lastSA+height[curRank]] != 124 objCoded[curSA+height[curRank]] ) 125 break; 126 } 127 } 128 } 129 } 130 131 typedef long long int64; 132 133 #include <iostream> 134 135 int main() 136 { 137 input(); 138 buildSuffixArray(); 139 buildHeight(); 140 141 int64 ans=0; 142 143 for(int i=1;i<=objLen;i++) 144 ans+=(objLen-suffixArray[i]+1)-height[i]; 145 146 std::cout<<ans<<"\n"; 147 return 0; 148 }
接下来,我们将对SA和rank的构造过程进行解析。
1 const int maxN=200005; 2 3 int suffixArray[maxN]; //1-based 4 int suffixRank[maxN]; //1-based 5 int height[maxN]; //LCP length of SA[i] and SA[i-1] 6 7 char objStr[maxN]; 8 int objCoded[maxN]; //begin with objCoded[1] 9 int objLen; 10 11 inline int codeChar(char x) 12 { 13 return x+1-‘a‘; 14 } //range:[1..26] 15 16 void input() 17 { 18 scanf("%s",objStr); 19 objLen=strlen(objStr); 20 21 for(int i=1;i<=objLen;i++) 22 objCoded[i]=codeChar(objStr[i-1]); 23 objCoded[objLen+1]=-1; 24 }
suffixArray(SA)就是后缀数组本身,suffixArray[i]=x,表示从小到大(字典序)第i个后缀从第x个字符开始,也就是“排第几的是谁”
以下为了叙述方便,我们用“后缀u”(u为一个整数)这样的说法代指“以第u个字符开始的后缀”
suffixRank(SR)是后缀数组的逆映射,若suffixRank[i]=x,则suffixArray[x]=i,表示以第i个字符开头的后缀能排第x位,也就是”你排第几“
height[i]记录后缀SA[i]和后缀SA[i-1]的LCP(Longest Common Prefix,最长公共前缀)长度。即排第i的后缀和排第i-1的后缀的LCP长度
objStr是我们要操作的目标字符串,objCoded则是”编码“后的串(我们假定字符集为小写英文字母)
当然如果不需要再对objStr本身进行操作(比如输出某个字串本身)的话,objCoded数组其实也可以省略掉
在objCoded的结尾,我们用-1代指‘/0‘(字符串结束符)
为了方便,我们将目标串的长度objLen存放到全局变量中,并且规定objCoded的下标从1开始
1 const int alphabetSize=26; 2 3 int charCount[alphabetSize+1]; 4 5 int secondKey[maxN]; //use suffixArray[] itself as firstKey 6 int radixCount[maxN]; 7 int suffixTemp[maxN];
这些变量的含义我们会在讲解buildSuffixArray()过程中予以说明(现在说了反正也没用(*´∇`*))
构建SA的过程只需4个辅助数组,而且与字符串规模相当的只有3个,另一个非常小,空间开销几乎可以忽略
“另一个非常小”的前提是字符集很小,不过在OI/ACM范畴内,它通常不会超过ASCII的值域(除非在某些问题中把数列当成串处理,那样的话“字符集”就会与objLen同阶)
在这3个“大”数组中,有一个实际上是可以省略的,所以真正必需的辅助空间实际上只有2N加上一点零头
我们将使用倍增算法构造SA数组。它的时间复杂度是O(n log n)
SA的O(n)构造算法(DC3)在这里不再赘述,它的常数因子巨大,所以时间效率实际上优势不是很大,而且其空间开销也比倍增算法大的多
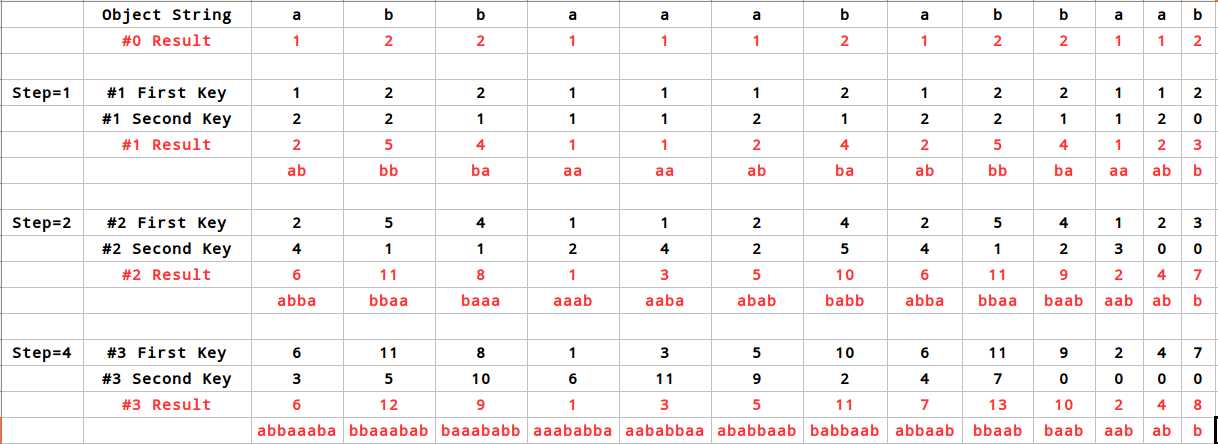
图为利用倍增算法求suffixRank数组的过程。
倍增算法的基本思路是:对于每一个后缀,第i次比较长度为step=2^i的前缀。如果该后缀长度小于step,用0作为第二关键字,直到:
(1)step>=objLen
(2)step<objLen,但排序的结果已经两两互异,这样的话再进行下去也没有意义了
0比charCoded的最小值1还要小,所以用0作为“填充物”,可以使末尾较短的(后缀的)前缀字典序较小。
每次比较时,把suffixRank[i]作为第一关键字,把suffixRank[i+step]作为第二关键字,然后进行排序
排序可以用快排实现,时间复杂度为O(n log n),乘以倍增的O(log n),总的时间复杂度就是O(n log^2 n)
更好的做法是基数排序,时间复杂度为O(n)
算法流程(伪代码):
首先把字符本身的排名作为suffixRank的初值
for(int step=1;step<objLen;step<<=1)
构建二元组P[i]={suffixRank[i],suffixRank[i+step]}(i+step>objLen时用0补充),对P[]进行基数排序
先按第二关键字得到suffixTemp序列,使得:
若suffixTemp[i]=x,则以第二关键字升序排序后,P[x]排在第i位
然后按第一关键字得到suffixArray(中间结果)
for(int i=objLen;i;i--)
记cur=suffixTemp[i],按基数排序的规则分配P[cur],使得第一关键字相同时,第二关键字大的放在后面
根据当前的suffixArray求出下一步的suffixRank
for(int i=1;i<=objLen;i++)
记cur=suffixArray[i],last=suffixArray[i-1]
若i==1,则令suffixRank[cur]=1,否则:
若P[cur]==P[last],则令suffixRank[cur]=suffixRank[last]
否则,令suffixRank[cur]=i,使得suffixRank[cur]>suffixRank[last]
1 memset(charCount,0,sizeof(charCount)); 2 3 for(int i=1;i<=objLen;i++) 4 ++charCount[objCoded[i]]; 5 6 for(int i=2;i<=alphabetSize;i++) 7 charCount[i]+=charCount[i-1]; 8 9 for(int i=1;i<=objLen;i++) 10 suffixRank[i]=charCount[objCoded[i]];
在”正式“开始基数排序之前,我们需要一个倍增的”基石“,即预先处理step=0的情形(也就是对字符本身排序)
这里则是用了计数排序(和基数排序有一些差异,尽管都是分配式排序而且汉语读音都完全一样)的思想
细心的话会发现按上面代码排出来的SR初值和图中给的不太一样:

事实上这无关紧要,因为此时我们只需要知道一个相对的大小关系,所以两种标号方式是等价的
1 for(int step=1;step<objLen;step<<=1) 2 { 3 for(int i=1;i<=objLen;i++) 4 secondKey[i]=(i+step<=objLen)?suffixRank[i+step]:0; 5 6 memset(radixCount,0,sizeof(radixCount)); 7 8 for(int i=1;i<=objLen;i++) 9 ++radixCount[secondKey[i]]; 10 11 for(int i=1;i<=objLen;i++) 12 radixCount[i]+=radixCount[i-1]; 13 14 for(int i=objLen;i;i--) 15 { 16 int pos=radixCount[secondKey[i]]--; 17 suffixTemp[pos]=i; 18 }
我们把基数排序的过程分成了两部分。
第一个循环用来比较secondKey(也就是第二关键字)。
这个数组可以省掉,secondKey可以即时计算出来,如果省掉的话辅助空间就成了2N
之后3个循环就是第一趟基数排序的过程,结果暂时放在suffixTemp数组内

这个suffixTemp就是第二趟基数排序的处理序列(仍然是倒序遍历),suffixTemp[i]=x表示第二关键字排第i位的二元组位于第x个位置
是不是和suffixArray的含义很像?实际上,我们求的这个suffixTemp数组就是suffixArray的中间结果
根据基数排序的实现原理,由于我们是对suffixTemp倒序处理的,所以(第一关键字相同时)第二关键字较大的会被放到相对靠后的位置
这样在第一关键字排好序的同时,第二关键字也会处于合适的位置
1 memset(radixCount,0,sizeof(radixCount)); 2 3 for(int i=1;i<=objLen;i++) 4 ++radixCount[suffixRank[i]]; 5 6 for(int i=1;i<=objLen;i++) 7 radixCount[i]+=radixCount[i-1]; 8 9 for(int i=objLen;i;i--) 10 { 11 int& cur=suffixTemp[i]; 12 int pos=radixCount[suffixRank[cur]]--; 13 suffixArray[pos]=cur; 14 }
第二趟基数排序,依照第一关键字(就是上一步的suffixRank)
最后一次循环,我们利用了suffixTemp序列,使得第二关键字较大的尽可能先被处理,其位置就会相对靠后
这里我们将第二趟基数排序的结果放到了suffixArray中。suffixArray[pos]=cur的含义就是”排第pos个的后缀可能从cur开始“
此时的suffixArray只是一个中间结果

int last=suffixRank[suffixArray[1]]; suffixRank[suffixArray[1]]=1; bool finished=true; for(int i=2;i<=objLen;i++) { int& curPos=suffixArray[i]; int& lastPos=suffixArray[i-1]; int temp=suffixRank[curPos]; if(temp==last && secondKey[curPos]==secondKey[lastPos]) { suffixRank[curPos]=suffixRank[lastPos]; finished=false; } else suffixRank[curPos]=i; last=temp; } if(finished) break; }
最后就是计算新的suffixRank数组。
这里实际上略微用到了SA和SR互为反函数的关系。但由于此时的suffixArray不一定是真正的SA,所以还需要进行比较
这一步得到的suffixRank可能会有相等的值(表示后缀i和后缀i+step在当前比较的范围内是相等的),所以此时的SR可能只是中间结果
这里用到了一个小优化:如果suffixRank没有相等的值,就说明我们已经得到了suffixRank(顺便也有suffixArray)的最终结果,此时直接跳出循环即可
小细节(节省空间需要)留给读者推敲
至此suffixArray和suffixRank的构造工作已经完成。它们已经可以用来处理简单的字符串问题
但是只有SA和rank数组,我们能处理的问题十分有限,所以我们还需要一个强大的工具——height数组
在下一篇博文中,我们不仅会对height[]的构造过程进行解析,而且会通过一些例题,初步展现height数组的威力
————To be continued————
后缀数组(Suffix Array)模板及简析——Part 1:构建SA和rank数组
标签:
原文地址:http://www.cnblogs.com/Onlynagesha/p/5437327.html