标签:
对一个数组中的元素按照顺序构建二叉树,就形成了一个(二叉)堆。(二叉树是虚拟的,并不是真的建立二叉树)
表示堆的数组A有两个重要属性:A.heapSize,表示堆里面有多少元素,数组里有多少元素在堆里
A.length,表示数组长度
例如数组A= {1,2,3,4,5,6,7,8,9,10},此时A.heapSize = A.length。除了最后一层之外,这个二叉树是完满的
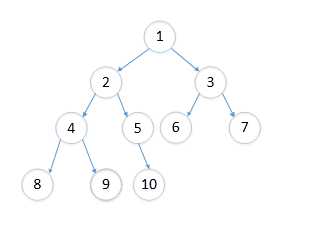
最大堆:父节点的值总是不小于子节点的值,反应在数组中就是A[i]>=A[2i+1] && A[i]>=A[2i+2],如果2i+2<A.size的话
最小堆:父节点的值总是不大于子节点的值,反应在数组中就是A[i]<=A[2i+1] && A[i]<=A[2i+2],如果2i+2<A.size的话,上图就是一个最小堆
堆排一般用最大堆,输出升序数组,最小堆用于优先队列。
堆排的时间复杂度是O(nlgn)
我写的是最小堆排序,输出降序数组
//=================== 最小堆维护 ================== // 调整根节点为arr[i]的子树顺序,将最小的节点放到根节点位置 // 递归调整被置换的子节点 void minHeapfy(vector<int> &arr, int i, int heapSize){ int left = 2 * i + 1; //对于arr[i],它的左孩子是arr[2i+1]右孩子是arr[2i+2] int right = 2 * i + 2; int least = i; if (left < heapSize && arr[left] < arr[least]) least = left; if (right < heapSize && arr[right] < arr[least]){ least = right; } if (least != i){ int temp = arr[i]; arr[i] = arr[least]; arr[least] = temp; minHeapfy(arr, least, heapSize); //如果子树发生变动,递归调整有变动的子节点 } } //=============== 建立最小堆 ================ // 利用minHeapfy调整每一棵子树,arr中arr[arrSize/2:]的元素都是叶子节点 void buildMinHeap(vector<int> &arr){ int heapSize = arr.size(); for (int i = heapSize/2-1; i >= 0; i--){ minHeapfy(arr, i, heapSize); } } // ================ 输出堆排结果 ==================== //由于根节点总是全堆最小的,每次置换根节点与最后一个节点 //对被置换之前的数组进行最小堆建立 void heapSort(vector<int> &arr){ int heapSize = arr.size(); buildMinHeap(arr); for (int i = heapSize - 1; i >= 0; i--){ int temp = arr[0]; //置换根节点元素和当前数组最后一个元素 arr[0] = arr[i]; arr[i] = temp; heapSize -= 1; minHeapfy(arr, 0, heapSize); //对有序元素之前的节点建立最小堆 } } int _tmain(int argc, _TCHAR* argv[]) { vector<int> primes = { 4, 1, 3, 2, 16, 9, 10, 14, 8, 7 }; heapSort(primes); for (int i = 0; i < primes.size(); i++){ cout << primes[i] << endl; } system("pause"); return 0; }
标签:
原文地址:http://www.cnblogs.com/Chilly2015/p/5438178.html