标签:
转载自:http://www.tuicool.com/articles/EnMFFja
原创:kuangbin
题意:
一个有向图,求:
1) 至少要选几个顶点,才能做到从这些顶点出发,可以到达全部顶点
2) 至少要加多少条边,才能使得从任何一个顶点出发,都能到达全部顶点,即成为一个强连通分量
思路:
求完强连通分量后,缩点,计算每个点的入度,出度。
第一问的答案就是入度为零的点的个数,
第二问就是max(n,m) 入度为零的个数为n, 出度为零的个数为m
思路详解:
1. 求出所有强连通分量
2. 每个强连通分量缩成一点,则形成一个有向无环图DAG。
3. DAG上面有多少个入度为0的顶点,问题1的答案就是多少
在DAG上要加几条边,才能使得DAG变成强连通的,问题2的答案就是多少
加边的方法:
要为每个入度为0的点添加入边,为每个出度为0的点添加出边
假定有 n 个入度为0的点,m个出度为0的点,如何加边?
把所有入度为0的点编号 0,1,2,3,4 ....N -1
每次为一个编号为i的入度0点可达的出度0点,添加一条出边,连到编号为(i+1)%N 的那个出度0点,
这需要加n条边
若 m <= n,则
加了这n条边后,已经没有入度0点,则问题解决,一共加了n条边
若 m > n,则还有m-n个入度0点,则从这些点以外任取一点,和这些点都连上边,即可,这还需加m-n条边。
所以,max(m,n)就是第二个问题的解
此外:当只有一个强连通分支的时候,就是缩点后只有一个点,虽然入度出度为0的都有一个,但是实际上不需要增加清单的项了,所以答案是1,0;
Tarjan算法浅解:
1.过程:
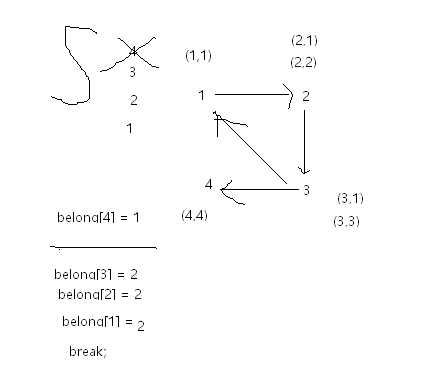
(1)dfn[i]表示dfs时达到顶点i的时间戳
low[i]表示i所能直接或间接达到 时间最小的顶点(比如上图 3->1 low[3] = 1)
(2)time初始化为0,在dfs遍历到u时,low[u]=dfn[u]=time++,u入栈
扫描u的邻接顶点v,如果 v没有被访问则dfs(v);
low[u]=min(low[u],low[v])
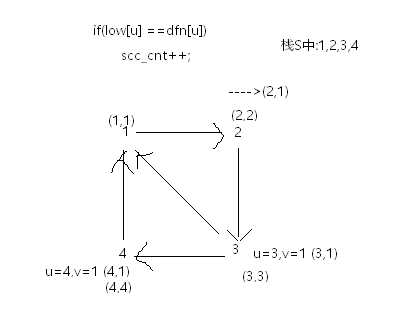
如果邻接顶点在此次已经被扫描:即dfn[v] != 0 和 belong[v] == 0 , low[u] = min(low[u],dfn[v]);
如果low[v]=dfn[v]时,栈里v以及v以上的顶点全部出栈,且刚刚出栈的就是一个极大强连通分量。
2.大概原理:
填坑......
代码:
1 //#include<bits/stdc++.h> 2 #include<vector> 3 #include<algorithm> 4 #include<cstring> 5 #include<cstdio> 6 #include<stack> 7 using namespace std; 8 typedef long long ll; 9 10 const int maxn = 100 + 10; 11 12 vector<int> G[maxn]; 13 int n,dfn[maxn],low[maxn],belong[maxn],dfs_clock,scc_cnt; 14 stack<int> S; 15 16 /** 17 18 Tarjan算法 19 20 */ 21 22 void dfs(int u){ 23 dfn[u] = low[u] = ++dfs_clock; 24 S.push(u); 25 for(int i = 0 ; i < G[u].size() ; i ++){ 26 int v = G[u][i]; 27 if(!dfn[v]){ 28 dfs(v); 29 low[u] = min(low[u],low[v]); 30 }else if(!belong[v]){ 31 low[u] = min(low[u],dfn[v]); 32 } 33 } 34 if(low[u] == dfn[u]){ 35 scc_cnt++; 36 for(;;){ 37 int x = S.top(); S.pop(); 38 belong[x] = scc_cnt; 39 if(x == u) break; 40 } 41 } 42 } 43 44 void scc(int n){ 45 dfs_clock = scc_cnt = 0; 46 memset(dfn,0,sizeof(dfn)); 47 memset(belong , 0 ,sizeof(belong)); 48 for(int i = 0 ; i < n ; i ++) 49 if(!dfn[i]) dfs(i); 50 51 } 52 53 int main(){ 54 int x; 55 while(scanf("%d",&n) != EOF && n){ 56 for(int i = 0 ; i <= n ; i ++) G[i].clear(); 57 for(int i = 0 ; i < n ; i ++){ 58 while(scanf("%d",&x),x){ 59 --x; 60 G[i].push_back(x); 61 } 62 } 63 scc(n); 64 if(scc_cnt == 1){ 65 printf("1\n0\n"); 66 continue; 67 } 68 int in[maxn],out[maxn],in_tot = 0 , out_tot = 0; 69 memset(in,0,sizeof(in)); 70 memset(out,0,sizeof(out)); 71 for(int i = 0 ; i < n ; i ++){ 72 for(int j = 0 ; j < G[i].size() ; j ++){ 73 int v = G[i][j]; 74 /** 75 遍历每个点. 76 遍历与该点相连的点 77 判断两个点是否同一个连通分量 78 如果不是,则改变缩点后的出入度 79 80 */ 81 if(belong[i] != belong[v]){ 82 out[ belong[i] ] ++; 83 in [ belong[v] ] ++; 84 } 85 } 86 } 87 for(int i = 1 ; i <= scc_cnt ; i ++){ 88 if(!in[i]) in_tot++; 89 if(!out[i]) out_tot++; 90 } 91 92 printf("%d\n%d\n",in_tot,max(in_tot,out_tot)); 93 } 94 return 0; 95 }
POJ1236 (Network of Schools,Tarjan,强连通分量)
标签:
原文地址:http://www.cnblogs.com/zstu-jack/p/5440212.html