标签:
1. 中缀到后缀的手工转换
(1)按优先级给表达式加括号
(2)从内向外将运算符移动对应的括号后面
(3)去括号,即可得到后缀表达式(如下图,图中数字表示转换顺序)
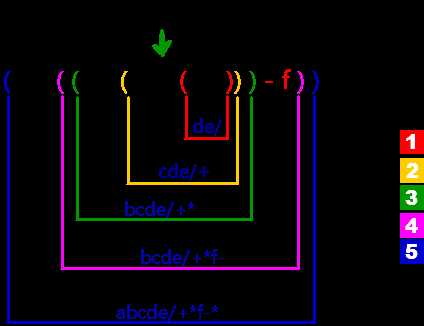
2. 后缀表达式求值
2.1 图解后缀表达式求值过程
(1)从左向右扫描后缀表达式。
(2)遇到数字直接进栈
(3)重点在于遇到运算符时,要找到其左右操作数。(此图中有5个运算符,分别是*、/、-、*、+)
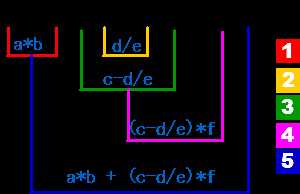
2.2 求值步骤(利用栈来进行运算,注意栈只用来保存操作数,并不保存操作符)
(1)当前元素为数字:进栈
(2)当前元素为运算符:
①从栈中弹出右操作数(注意,先弹出右操作数,再弹出左操作数)
②从栈中弹出左操作数
③根据符号进行运算
④将运算结果压入栈中
(3)遍历结束:栈中的唯一数字为运算结果
2.3 伪代码

3. 除0问题
(1)与数学计算相关的算法都需要考虑除0的情况
(2)若是浮点运算,避免代码中直接与0做相等比较

【编程实验】计算后缀表达式
//QCalculatorDec.h

#ifndef QCALCULATORDEC_H #define QCALCULATORDEC_H #include <QString> #include <QStack> #include <QQueue> class QCalculatorDec { protected: QString m_exp; QString m_result; bool isDigitOrDot(QChar c); bool isSymbol(QChar c); //操作符或左右括号 bool isSign(QChar c); //符号位+或- bool isNumber(QString s); bool isOperator(QString s); bool isLeft(QString s); bool isRight(QString s); int priority(QString s); //操作符的优先级 //识别各个token QQueue<QString> split(const QString& exp); //中缀表达式转换后缀表达式 bool transform(QQueue<QString>& exp, QQueue<QString>& output); //判断括号是否匹配 bool match(QQueue<QString>& exp); //重载函数 QString calculate(QQueue<QString>& exp);//对后缀表达式求值 QString calculate(QString l, QString op, QString r);//根据运算符,对左右操作数取值 public: QCalculatorDec(); ~QCalculatorDec(); bool expression(const QString& exp); //QString expression(); QString result(); }; #endif // QCALCULATORDEC_H
//QCalculatorDec.cpp
#include "QCalculatordec.h" #include <QDebug> QCalculatorDec::QCalculatorDec() { m_exp = ""; m_result = ""; } QCalculatorDec::~QCalculatorDec() { } bool QCalculatorDec::isDigitOrDot(QChar c) { return ((‘0‘ <= c) && (c <= ‘9‘)) || (c == ‘.‘); } bool QCalculatorDec::isSymbol(QChar c) { return isOperator(c) || (c ==‘(‘) || (c == ‘)‘); } bool QCalculatorDec::isSign(QChar c) { return (c == ‘+‘) || (c == ‘-‘); } bool QCalculatorDec::isNumber(QString s) { bool ret = false; s.toDouble(&ret); //将字符串转为数字 return ret; } bool QCalculatorDec::isOperator(QString s) { return (s == "+") || (s == "-") ||(s == "*") ||(s == "/"); } bool QCalculatorDec::isLeft(QString s) { return (s == "("); } bool QCalculatorDec::isRight(QString s) { return (s == ")"); } //操作符的优先级 int QCalculatorDec::priority(QString s) { int ret = 0; //非运算符(含括号)优先级最低,为0 if((s == "+") || (s =="-")) { ret = 1; }else if((s == "*") || (s == "/")) { ret = 2; } return ret; } //对用户输入的表达式进行分析与求解 bool QCalculatorDec::expression(const QString &exp) { bool ret =false; QQueue<QString> spExp = split(exp); QQueue<QString> postExp; //后缀表达式 m_exp = exp; if(transform(spExp, postExp)) { m_result = calculate(postExp);//对后缀表达式进行求值 ret = (m_result != "Error"); } else { m_result = "Error"; } return ret; } QString QCalculatorDec::result() { return m_result; } QQueue<QString> QCalculatorDec::split(const QString& exp) { QQueue<QString> ret; QString num = ""; QString pre = ""; for(int i=0; i<exp.length(); i++) { //数字或小数点 if(isDigitOrDot(exp[i])){ num +=exp[i]; pre = exp[i]; //标识符(操作符、左右括号),其它字符(如空格)会被跳过 }else if(isSymbol(exp[i])){ //遇标识符时,表示读到的己经不是数字了,就将num分离并保存起来 if(!num.isEmpty()) { ret.enqueue(num);//num进队列,保存起来 num.clear(); } //如果当前这个非数字的标识符是+或-,则进一步判断是正负号,还是运算符 //当+或-的前一个有效字符为空、左括号或运算符时,这时他们表示正负号。如+9、(-3、5- -3 if(isSign(exp[i]) && ((pre =="") || (pre == "(") || isOperator(pre))) { num +=exp[i]; } else { //运算符或左右括号等符号进队列 ret.enqueue(exp[i]); } pre = exp[i]; //读完一个字符 } } //读完所有的字符,最后一个数字型的串入队列 if(!num.isEmpty()) { ret.enqueue(num); } return ret; } //中缀表达式转换后缀表达式(利用栈来实现中缀转后缀 bool QCalculatorDec::transform(QQueue<QString>& exp, QQueue<QString>& output) { bool bRet = match(exp); QStack<QString> stack; //利用栈来保存操作符 output.clear(); //依次读入各个token while (bRet && !exp.isEmpty()) { QString e = exp.dequeue(); //出队列 if(isNumber(e)) { output.enqueue(e); //数字,直接输出(到队列) }else if(isOperator(e)) //操作符和括号 { //当前运算符的优先级低于栈顶元素(外面水位低,水出湖) while(!stack.isEmpty() && (priority(e) <= priority(stack.top()))) { output.enqueue(stack.pop()); } //压入当前操作符 stack.push(e); }else if(isLeft(e)) //左括号,直接进栈 { stack.push(e); }else if(isRight(e)) //右括号,弹出栈中元素,直到遇到左括号 { while (!stack.isEmpty() && !isLeft(stack.top())) { output.enqueue(stack.pop()); } if(!stack.isEmpty()) { stack.pop();//弹出左括号(丢弃) } }else { bRet = false; } } //将栈中所有剩余的符号弹出 while (!stack.isEmpty()) { output.enqueue(stack.pop()); } if(!bRet) //如果转换时出错,清空输出内容 { output.clear(); } return bRet; } //判断括号是否匹配 bool QCalculatorDec::match(QQueue<QString>& exp) { bool bRet = true; int len = exp.length(); QStack<QString> stack; for(int i=0; i<len; i++) { if(isLeft(exp[i])) //左括号,则进栈 { stack.push(exp[i]); } else if(isRight(exp[i])) //右括号 { //因左括号必定先于右括号出现,否则是错误的表达式 if(!stack.isEmpty() && isLeft(stack.top())) { //遇到一个右括号,则弹出栈顶的左括号与之匹配。 stack.pop(); } else { //遇到右括号时,匹配不成功的原因: //1.栈己经是空的,表示没有左括号可以匹配了 //2.当栈顶元素不是左括号 bRet = false; break; } } } //只有当栈己经空了,并且所有右括号都找到匹配,才返回匹配成功 return bRet && stack.isEmpty(); } //利用栈对后缀表达式求值 QString QCalculatorDec::calculate(QQueue<QString>& exp) { QString ret = "Error"; QStack<QString> stack; //栈 while(!exp.isEmpty()) { QString e = exp.dequeue();//当前token if(isNumber(e)) { stack.push(e); //数字直接进栈 } else if(isOperator(e)) { QString rp = !stack.isEmpty()? stack.pop() : ""; //右操作数 QString lp = !stack.isEmpty()? stack.pop() : ""; //左操作数 QString result = calculate(lp, e, rp); if(result != "Error") { stack.push(result); } else { break; } } else //非法token(即不是数字或运算符) { break; } } if(exp.isEmpty() &&(stack.size() == 1) && isNumber(stack.top())) { ret = stack.top(); } return ret; } //根据运算符,对左右操作数取值 QString QCalculatorDec::calculate(QString l, QString op, QString r) { QString ret = "Error"; if(isNumber(l) && isNumber(r)) { double lp = l.toDouble(); double rp = r.toDouble(); if(op == "+") { ret.sprintf("%f", lp + rp); } else if(op == "-") { ret.sprintf("%f", lp - rp); } else if(op == "*") { ret.sprintf("%f", lp * rp); } else if(op == "/") { const double P = 0.000000000000001; if((-P < rp) && (rp < P)) //除数不能为0 { ret = "Error"; } else { ret.sprintf("%f", lp / rp); } } else { ret = "Error"; } } return ret; }
4. 小结
(1)计算方法由3个不同的子算法构成
(2)Qt项目在整体上采用面向对象分析与设计
(3)局部的算法设计依计采用面向过程的方法完成
(4)Qt开发是各种开发技术的综合运用
标签:
原文地址:http://www.cnblogs.com/5iedu/p/5447767.html