标签:
问题:
给出方程f(x) = x^3+10x-20,求该方程在(1,2)上的根,其精度不小于10^-4
看似很简单的一个小问题,其实有很有细节值得注意,先给出代码
方法一:
#include <stdio.h> #include <math.h> double f(double x) { return x*x*x+10*x-20; } int main() { double l,r,mid,ans; l = 1; r = 2; while(1) { mid = (l+r)/2; double cnt = f(mid); if(fabs(cnt) <= 0.0001) { ans = mid; printf("%lf\n",cnt); break; } if(cnt > 0) r = mid; else l = mid; } printf("%.4lf\n",ans); return 0; }
方法二:
#include <stdio.h> #include <math.h> double ans; double f(double x) { return x*x*x+10*x-20; } void m(double l,double r) { double mid = (l+r)/2; double cnt = f(mid); if(fabs(cnt) <= 1e-4) { ans = mid; return ; } if(cnt > 0) m(l,mid); else m(mid,r); } int main() { m(1,2); printf("%.4lf\n",ans); return 0; }
两种方法没有本质上的区别,算法实质是一样的,只是在程序实现手段上稍有不同,方法一用的循环,而方法二用的递归。
有这么几点需要注意
(1)如何确定精度小于1e-4?
首先我们要想明白,我们要确定的是“根”的精度,即让f(ans)=0的那个ans的计算值和真理值得差不大于1e-4,我们不知道所谓的真理值是多少,但是我们能确认他的函数值,即0,因此这个问题就转化成了我们计算得到的值ans的函数值f(ans)与0的绝对值差要不大于1e-4,因而我们就可以每次求出当前的mid即可能中点的值,看看他与0的差距是否小于等于1e-4,如果是,这个mid就是我们最终要求的结果。
(2)关于每次迭代l和r的值的确定,暂时没有发现什么一般性的规则,只是在这道题中,我们可以用图像很直观的表达出来l和r的更替规律
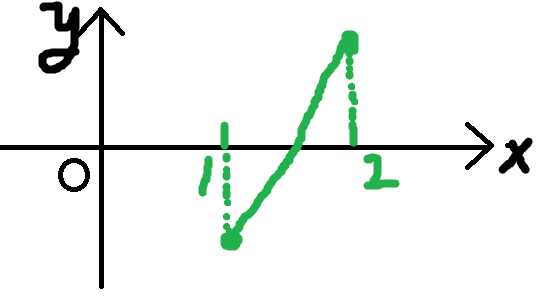
首先很容易可以求出f(x)在定义域上为单调递增,然后在x=1的值是负的,在x=2的值是正的,那么二者之间就必然只有一个根了,因此如果当前求得的f(ans)的值为正数和负数的情况,根据该图,我们都能很清晰的看出来到底该把谁给赋值。
标签:
原文地址:http://www.cnblogs.com/immortal-worm/p/5450870.html