标签:
尝试表达
本人试着去表达约瑟夫环问题:一群人围成一个圈,作这样的一个游戏,选定一个人作起点以及数数的方向,这个人先数1,到下一个人数2,直到数到游戏规则约定那个数的人,比如是3,数到3的那个人就离开这个游戏;按这样的规则,剩下一个人,游戏就结束,这个人就为赢家。(读者可以试着表达,不认同,直接忽略)
抽象分析
这个人就是一个数据个体,数据结点,数据元素。上面产生的数据结构为:单方向循环的链。可以用链表实现,也可以用数组来实现。
链表到数组的迁移
|
|
人(数据元素、 数据结点、数据个体) |
结点关系 (结构关系 结点移动) |
范型“指针”定义 :能够定位到下一个结点(变) |
“指针“ |
移到下一个结点 拿到下一个结点的”指针“即可,一般都有作“移动”变量,移动变量变,就相当于移动。 |
删除结点 |
|
数组 |
连续的数组元素(基本数据类型,机构体) |
数组元素里面保存有下个结点元素的数组元素下标position。 |
arrayname固定的,只要给出position,就可以算是定位到数组元素 |
≈poisiton [] |
move =array[move] |
元素内容 = -1 (数组的大小固定) |
|
链表 |
离散的链表结点(结构体) |
结构体里面保存有下一个结点的指针 node* next |
poiter直接定位到结点,在结合常员变量,就可以拿到数据 |
=poiter -> |
move = move -> next |
销毁 |
画图分析:
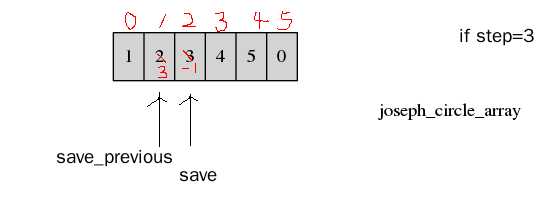
代码实现:
#include<stdio.h> #include<stdlib.h> /*Function:遍历数组实现的约瑟夫环。traverse_joseph_circle_array *param:int[] array,int tail *return: void * 假设是用数组实现的约瑟夫环链一定存在。 * */ void traverse_joseph_circle_array (int array[], int tail ){ //数组保存的是下个结点的“指针”,只不过这个指针要通过array才能够拿到结点的元素,因为array是固定的,只要变换指针就能够变换结点。 int move= array [tail] ;//从头开始遍历 do{ printf ("%d ;",move) ;//数组的元素位置(下标号)就代表这个结点,链表是通过结点里面的元素, move = array[move]; }while ( move != array [tail]); printf("\n"); } /*Function:约瑟夫环问题的数组实现。eliminate_array *param:int[]array,int tail, int step *return: void * */ void eliminate_array1 (int array[], int tail ,int step ){ int move = tail ; int save_previous = move ; int count = 0 ; while(move != array[move]){ save_previous = move ; move = array [move]; if(++ count == step){ //数数 array[save_previous] = array[move] ;//重构链 if( tail == move) tail = save_previous;//销毁前,判断要不要更新新约瑟夫环 printf("当前要删除的结点:%d \n",move);//销毁前告知用户 array[move]= -1 ;//销毁 printf("当前的约瑟夫环为:\n") ; traverse_joseph_circle_array (array,tail); count = 0 ; move = save_previous ; } } } /*Function:约瑟夫环问题的数组实现。eliminate_array *param:int[]array,int tail, int step *return: void * */ void eliminate_array2 (int array[], int tail ,int step ){ int move = tail ; int save_previous = move ; int count = 0 ; //每执行一此循环,删除一个结点。 while (move != array[move]){ save_previous = move ; move = array[move]; // 移动到要删除的结点 for (count = 0 ; count < step -1 ; count++){ move = array[move] ; } //删除结点,重构约瑟夫环,更新tail array[save_previous] = array[move] ;//重构链 if( tail == move) tail = save_previous;//update tail printf("当前要删除的结点:%d \n",move);//销毁前告知用户 array[move]= -1 ;//销毁 printf("当前的约瑟夫环为:\n") ; traverse_joseph_circle_array (array,tail); //移动回消除结点的上一个结点,回到初态,即将进行下一轮的游戏。 count = 0 ; move = save_previous ; } } int main(){ //创建有6个结点的约瑟夫环int array[6]; int array[20]; int length = sizeof(array)/sizeof(int); int ctl ; for (ctl = 0 ; ctl < length -1 ;ctl ++){ array[ctl] = ctl + 1; } array [length -1] = 0 ; traverse_joseph_circle_array(array,length-1); int tail = length -1; //eliminate_array1(array ,tail ,3) ; eliminate_array2(array ,tail ,3) ; return 0 ; }
结果:
0 ;1 ;2 ;3 ;4 ;5 ;6 ;7 ;8 ;9 ;10 ;11 ;12 ;13 ;14 ;15 ;16 ;17 ;18 ;19 ; 当前要删除的结点:2 当前的约瑟夫环为: 3 ;4 ;5 ;6 ;7 ;8 ;9 ;10 ;11 ;12 ;13 ;14 ;15 ;16 ;17 ;18 ;19 ; 当前要删除的结点:5 当前的约瑟夫环为: 6 ;7 ;8 ;9 ;10 ;11 ;12 ;13 ;14 ;15 ;16 ;17 ;18 ;19 ; 当前要删除的结点:8 当前的约瑟夫环为: 9 ;10 ;11 ;12 ;13 ;14 ;15 ;16 ;17 ;18 ;19 ; 当前要删除的结点:11 当前的约瑟夫环为: 12 ;13 ;14 ;15 ;16 ;17 ;18 ;19 ; 当前要删除的结点:14 当前的约瑟夫环为: 15 ;16 ;17 ;18 ;19 ; 当前要删除的结点:17 当前的约瑟夫环为: 18 ;19 ; 当前要删除的结点:18 当前的约瑟夫环为: 19 ;
时间复杂度分析:
本人推荐使用第二种算法来作,对于时间复杂度,要通过逻辑思考,要删除(n-1)个结点,循环执行(n-1)次,内循环执行k=step 次,这个k可能很大;还有在外循环,与内循环无关的,必须执行的某些语句,执行次数为c,表达式为:(n-1)(k+c)=nk +nc -k -c ,表达为:n*k - c0 * n - c1 *k ,大O表达为:O(nk)
注意:感谢麦子学院出的精品课程。本人由于学业繁多,精力有限,水平不足,难免不出问题,请多多包涵,发现什么错漏,有什么建议,请留言私信qq:632929757。
标签:
原文地址:http://www.cnblogs.com/qingshenqin/p/5456579.html