标签:
一、理论概念
区域生长是按照事先定义的生长准则将一个像素或者子区域逐步聚合成一个完整独立的连通区域过程。对于图像感兴趣目标区域R,z为区域R上事先发现的种子点,按照规定的生长准则逐步将与种子点z一定邻域内符合相似性判据的像素合并成一个种子群以备下一阶段的生长,这样不断的进行循环生长直到满足生长停止条件为止,从而完成了对感兴趣区域由一个种子点生长为一个独立连通区域的过程。其中相似性判据可以是像素灰度值、颜色、纹理特征等图像信息。
因此区域生长算法一般分为三个步骤实现:
(1) 确定生长种子点
(2) 规定生长准则
(3) 确定生长停止条件
实际工程应用中区域生长算法常被用于对二值化图像指定连通区域的分割。图1以图文方式对区域生长算法的三步骤进行解释:
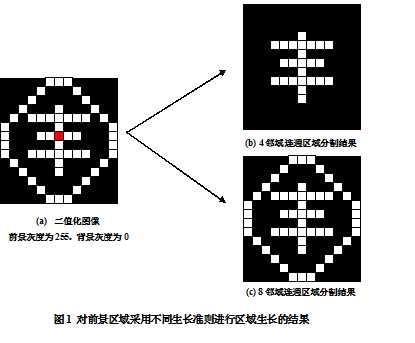
① 原始二值化图像(a)中的红色标注的像素为指定生长点;
② 图像(b)和(c)是采用不同生长准则进行区域生长的结果,其中图(b)是在4邻域下,待测像素与生长点像素灰度值相等的像素集合。正如图中所示第1次生长时,与生长点像素灰度相等的像素有上、下、左、右四个像素,接着第二次生长时,就由前一次已经生长的像素按照同样的准则进行下去,直到遇到图像边界或背景区域时生长停止。图(c)是在8邻域下,待测像素与生长点像素灰度值相等的像素集合。
二、MATLAB示例代码实现
2.1 主函数文件
%主文件 clc; clear all; close all; %申明全局变量 R:区域生长的结果图像;BW:二值化图像;counter:感兴趣连通区域的像素个数 %row:图像的行数;col:图像的列数 global R BW counter row col I = imread(‘E:\MATLAB仿真\fsr.bmp‘); I = I(:,:,1); [row,col] = size(I); figure,imshow(I); level = graythresh(I); BW = im2bw(I,level); figure,imshow(BW); [y0,x0] = getpts; x0 = uint32(x0); y0 = uint32(y0); counter = 0; R = zeros(row,col); R = uint8(R); fsrRegiongrow(x0,y0,4);% fsrRegiongrow1(x0,y0,4); figure,imshow(R);
2.2 函数模块1
function fsrRegiongrow(x0,y0,mode)
%功能: 通过函数递归方法对二值化图像指定连通区域实现区域生长
%输入参数: x0,y0表示生长点像素坐标,mode表示以多大邻域进行区域生长,常取mode = 4;mode = 8;
%输出参数: void
%作者&时间: 奔跑在湘边———2016年5月6日
global R BW counter row col
if 8 == mode
for i = -1 : 1
for j = -1 : 1
x1 = x0 + i;
y1 = y0 + j;
%生长准则:判断生长点8邻域内像素的各自灰度值是否与生长点所在像素灰度值相等
if x1 > 0 && x1 <= row && y1 > 0 && y1 <= col && BW(x1,y1) == BW(x0,y0) && 0 == R(x1,y1)
R(x1,y1) = 255;
counter = counter + 1;
fsrRegiongrow(x1,y1,mode);
end
end
end
elseif 4 == mode
for i = -1 : 1
x1 = x0 + i;
y1 = y0;
if x1 > 0 && x1 <= row && y1 > 0 && y1 <= col && BW(x1,y1) == BW(x0,y0) && 0 == R(x1,y1)
R(x1,y1) = 255;
counter = counter + 1;
fsrRegiongrow(x1,y1,mode);
end
end
x1 = x0;
y1 = y0 - 1;
if x1 > 0 && x1 <= row && y1 > 0 && y1 <= col && BW(x1,y1) == BW(x0,y0) && 0 == R(x1,y1)
R(x1,y1) = 255;
counter = counter + 1;
fsrRegiongrow(x1,y1,mode);
end
x1 = x0;
y1 = y0 + 1;
if x1 > 0 && x1 <= row && y1 > 0 && y1 <= col && BW(x1,y1) == BW(x0,y0) && 0 == R(x1,y1)
R(x1,y1) = 255;
counter = counter + 1;
fsrRegiongrow(x1,y1,mode);
end
end
end
2.3 函数模块2
function fsrRegiongrow1(x0,y0,mode)
%功能: 模拟栈的先进后出思路对二值化图像指定连通区域实现区域生长
%输入参数: x0,y0表示生长点像素坐标,mode表示以多大邻域进行区域生长,常取mode = 4;mode = 8;
%输出参数: void
%作者&时间: 奔跑在湘边———2016年5月6日
global R BW counter row col
zhan = zeros(row*col,2);%创建栈数组
pzhan = 1; %栈计数
zhan(pzhan,1) = x0;
zhan(pzhan,2) = y0;
R(x0,y0) = 255;
counter = 1;
if 8 == mode
while pzhan > 0
x1 = zhan(pzhan,1);%出栈
y1 = zhan(pzhan,2);
pzhan = pzhan - 1; %栈计数减一
for i = -1 : 1
for j = -1 : 1
%生长准则:判断生长点8邻域内像素的各自灰度值是否与生长点所在像素灰度值相等
if x1+i > 0 && x1+i <= row && y1+j > 0 && y1+j <= col && BW(x1+i,y1+j) == BW(x1,y1) && R(x1+i,y1+j) ~= R(x1,y1)
R(x1+i,y1+j) = R(x1,y1);
counter = counter + 1;
pzhan = pzhan + 1; %栈计数增一
zhan(pzhan,1) = x1 + i;%入栈
zhan(pzhan,2) = y1 + j;
end
end
end
end
elseif 4 == mode
while pzhan > 0
x1 = zhan(pzhan,1);
y1 = zhan(pzhan,2);
pzhan = pzhan - 1;
for i = -1 : 2 : 1
j = 0;
if x1+i > 0 && x1+i <= row && y1+j > 0 && y1+j <= col && BW(x1+i,y1+j) == BW(x1,y1) && R(x1+i,y1+j) ~= R(x1,y1)
R(x1+i,y1+j) = R(x1,y1);
counter = counter + 1;
pzhan = pzhan + 1;
zhan(pzhan,1) = x1 + i;
zhan(pzhan,2) = y1 + j;
end
end
for j = -1 : 2 : 1
i = 0;
if x1+i > 0 && x1+i <= row && y1+j > 0 && y1+j <= col && BW(x1+i,y1+j) == BW(x1,y1) && R(x1+i,y1+j) ~= R(x1,y1)
R(x1+i,y1+j) = R(x1,y1);
counter = counter + 1;
pzhan = pzhan + 1;
zhan(pzhan,1) = x1 + i;
zhan(pzhan,2) = y1 + j;
end
end
end
end
end
三、说明
在基于MATLAB7.11.0(R2010b)平台调用函数模块fsrRegiongrow时,MATLAB会弹出如下警告
??? Maximum recursion limit of 500 reached. Use set(0,‘RecursionLimit‘,N)
to change the limit. Be aware that exceeding your available stack space can crash MATLAB and/or your computer.
Error in ==> fsrRegiongrow
上述警告表示递归次数超出了MATLAB默认值,也就是说待处理的感兴趣连通区域像素个数太多(大于500),此时用户可以尝试通过提示的set函数来修改函数递归次数,但是本文通过测试发现如果递归次数超出1591时(不同的平台该值可能不同),MATLAB软件会自动立即关闭。总之,大量的递归调用会建立函数的副本,消耗大量的时间和内存,但是递归可以使得程序结构清晰易懂,所以本文给出函数递归的方法来实现区域生长只是提供一个思路,如果待处理的连通区域像素个数很多,调用fsrRegiongrow1函数就可以了!fsrRegiongrow1函数模块是在堆上创建栈数组模拟栈的先进后出思想来实现的,可以快速的实现区域生长。
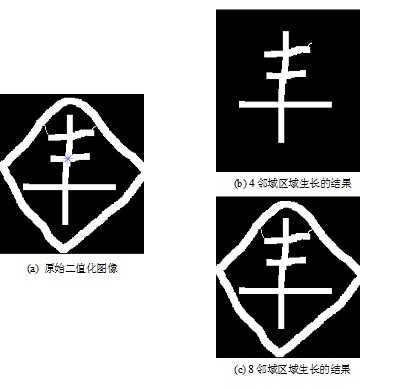
四、实验结果
标签:
原文地址:http://www.cnblogs.com/fengshengri/p/5467685.html