标签:
1.快速排序
不稳定
分而治之
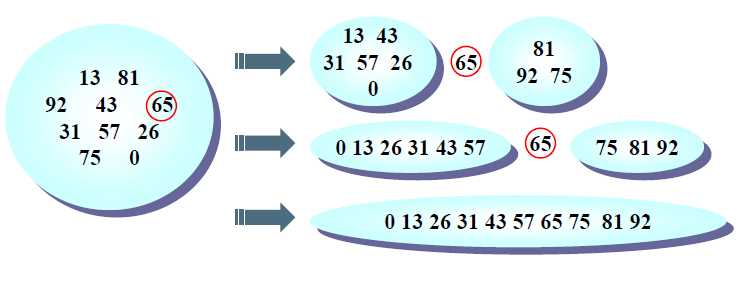
找主元pivot,小于主元划分为一个子集,大于主元的划分为一个子集
然后进行递归
最好情况:每次主元正好中分,T(N) = O( NlogN )
选主元 的方法有很多,这里用 取头、中、尾的中位数。
直接选A[0]为pivot,时间复杂度T ( N ) = O( N ) + T ( N–1 ) = O( N ) + O ( N–1 ) + T( N–2 ) = = O( N ) + O ( N–1 ) + …+ O( 1 ) = O( N^2 )
随机取pivot:rand()函数 也很费
取头、中、尾的中位数……
子集划分
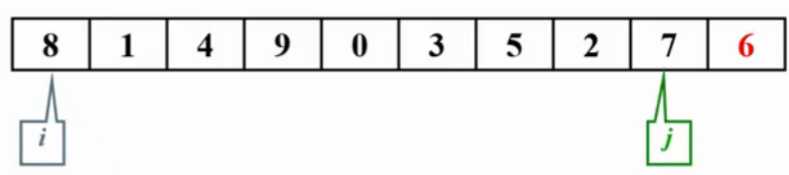
i指向8,j指向7.
8>6,i不动,7>6,j--;j指向2,2<6,j不动 交换8和2;

i++,i指向1,1<6,i++;i指向4,4<6,i++;i指向9,9>6,i不动;
j--,j指向5,5<6,j不动,交换5和9;
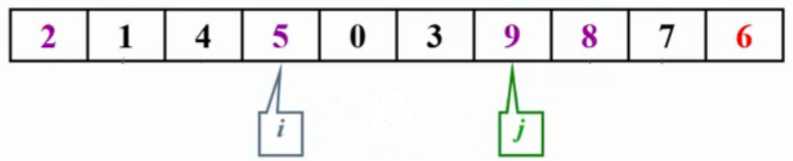
i++,i指向0,0<6,i++;i指向3,3<6,i++;i指向9,9>6,i不动;
j--,j指向3,3<6,j不动.
i>j,结束,6放到i位置,即6和9交换
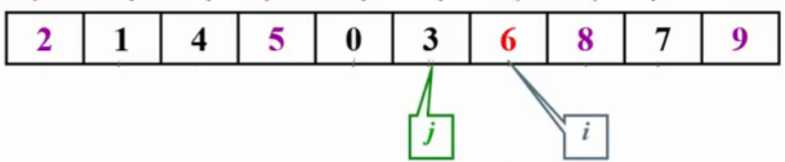
如果有元素正好等于pivot怎么办:
停下来交换:会产生很多不必要的交换。(一串相等的序列)
不理它,继续移动指针:pivot位置靠近一段,最糟糕会在最右边端,和pivot取A[0]一样,O( N^2 )
综合考虑,选第一种,停下来交换。
小规模数据的处理
快速排序的问题
用递归……
对小规模的数据(例如N不到100)可能还不如插入排序快
解决方案
当递归的数据规模充分小,则停止递归,直接调用简单排序(例如插入排序)
在程序中定义一个Cutoff的阈值

1 #include <stdio.h> 2 typedef int ElementType; 3 4 void Swap( ElementType *a, ElementType *b ) 5 { 6 ElementType t = *a; 7 *a = *b; 8 *b = t; 9 } 10 11 void InsertionSort(ElementType A[], int N) 12 { 13 int i; 14 for (int P = 1; P < N; P++ ) { 15 ElementType temp = A[P]; //取出未排序序列中第一个元素 16 for (i = P; i > 0 && A[i-1] > temp; i-- ) 17 A[i] = A[i-1]; //依次与已排序序列中元素比较并右移 18 A[i] = temp; 19 } 20 } 21 22 /* 快速排序 */ 23 ElementType Median3( ElementType A[], int Left, int Right ) 24 { 25 int Center = (Left+Right) / 2; 26 if ( A[Left] > A[Center] ) 27 Swap( &A[Left], &A[Center] ); 28 if ( A[Left] > A[Right] ) 29 Swap( &A[Left], &A[Right] ); 30 if ( A[Center] > A[Right] ) 31 Swap( &A[Center], &A[Right] ); 32 /* 此时A[Left] <= A[Center] <= A[Right] */ 33 Swap( &A[Center], &A[Right-1] ); /* 将基准Pivot藏到右边*/ 34 /* 只需要考虑A[Left+1] … A[Right-2] */ 35 return A[Right-1]; /* 返回基准Pivot */ 36 } 37 38 void Qsort( ElementType A[], int Left, int Right ) 39 { /* 核心递归函数 */ 40 int Pivot, Cutoff = 50, Low, High;//阈值的定义 41 42 if ( Cutoff <= Right-Left ) { /* 如果序列元素充分多,进入快排 */ 43 Pivot = Median3( A, Left, Right ); /* 选基准 */ 44 Low = Left; High = Right-1; 45 while (1) { /*将序列中比基准小的移到基准左边,大的移到右边*/ 46 while ( A[++Low] < Pivot ) ; 47 while ( A[--High] > Pivot ) ; 48 if ( Low < High ) Swap( &A[Low], &A[High] ); 49 else break; 50 } 51 Swap( &A[Low], &A[Right-1] ); /* 将基准换到正确的位置 */ 52 Qsort( A, Left, Low-1 ); /* 递归解决左边 */ 53 Qsort( A, Low+1, Right ); /* 递归解决右边 */ 54 } 55 else InsertionSort( A+Left, Right-Left+1 ); /* 元素太少,用简单排序 */ 56 } 57 58 void QuickSort( ElementType A[], int N ) 59 { /* 统一接口 */ 60 Qsort( A, 0, N-1 ); 61 } 62 63 int main() 64 { 65 int a[] = {34,8,64,51,32,21}; 66 QuickSort(a, 6); 67 for(int i = 0; i < 6; i++) 68 printf("%d ",a[i]); 69 return 0; 70 } 71 72 QuickSort
2.表排序
间接排序
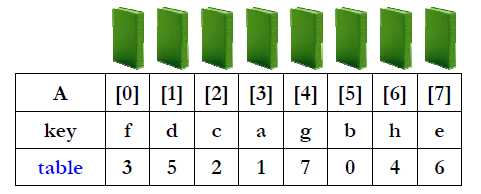
定义一个指针数组(下标)作为“表”(table)
如果仅要求按顺序输出,则输出:A[ table[0] ], A[ table[1] ], ……, A[ table[N-1] ]
物理排序
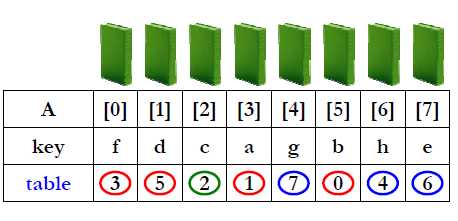
N个数字的排列由若干个独立的环组成
用temp记录初值 ,每次换位子修改table值,用if ( table[i] == i )判断一个环的结束
复杂度
最好情况:初始即有序
最坏情况:
有[N / 2]向下取整 个环,每个环包含2个元素
需要[N / 2]向下取整 次元素移动
T = O( m N ) ,m 是每个A元素的复制时间。
3.基数排序
桶排序:假设我们有N 个学生,他们的成绩是0到100之间的整数(于是有M = 101 个不同的成绩值)。如何在线性时间内将学生按成绩排序?
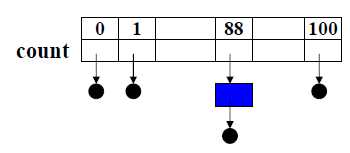
 T(N, M) = O( M+N )
T(N, M) = O( M+N )
当M>>N时,桶排序不合算
次位优先LSB
假设我们有N = 10 个整数,每个整数的值在0到999之间(于是有M = 1000 个不同的值)。
输入序列: 64, 8, 216, 512, 27, 729, 0, 1, 343, 125
用“次位优先”(Least Significant Digit) T=O(P(N+B))
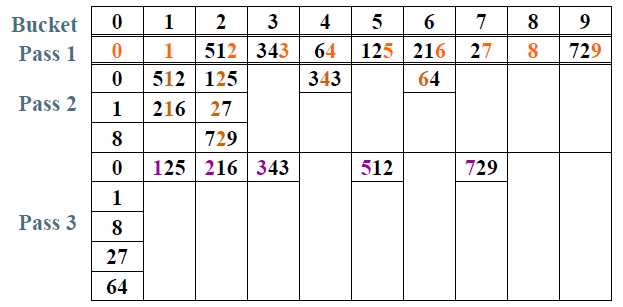
多关键字的排序
一副扑克牌是按2种关键字排序的
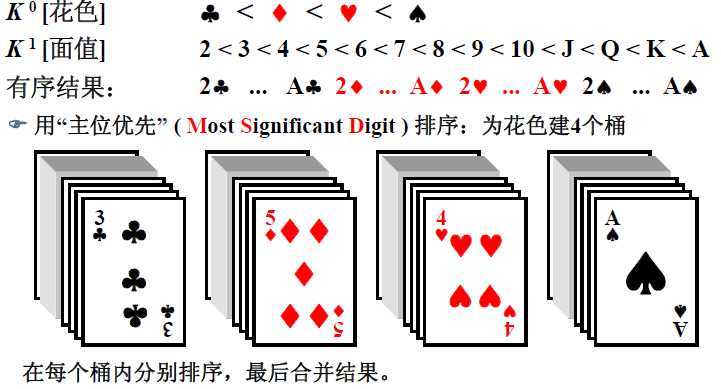
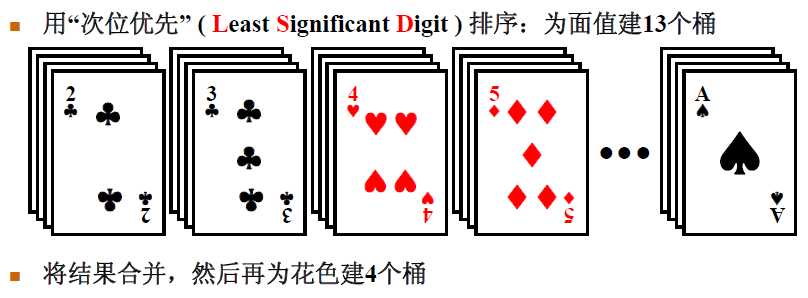

1 #include <stdio.h> 2 #include <stdlib.h> 3 4 typedef int ElementType; 5 6 /* 基数排序 - 次位优先 */ 7 8 /* 假设元素最多有MaxDigit个关键字,基数全是同样的Radix */ 9 #define MaxDigit 4 10 #define Radix 10 11 12 /* 桶元素结点 */ 13 typedef struct Node *PtrToNode; 14 struct Node { 15 int key; 16 PtrToNode next; 17 }; 18 19 /* 桶头结点 */ 20 struct HeadNode { 21 PtrToNode head, tail; 22 }; 23 typedef struct HeadNode Bucket[Radix]; 24 25 int GetDigit ( int X, int D ) 26 { /* 默认次位D=1, 主位D<=MaxDigit */ 27 int d, i; 28 29 for (i=1; i<=D; i++) { 30 d = X % Radix; 31 X /= Radix; 32 } 33 return d; 34 } 35 36 void LSDRadixSort( ElementType A[], int N ) 37 { /* 基数排序 - 次位优先 */ 38 int D, Di, i; 39 Bucket B; 40 PtrToNode tmp, p, List = NULL; 41 42 for (i=0; i<Radix; i++) /* 初始化每个桶为空链表 */ 43 B[i].head = B[i].tail = NULL; 44 for (i=0; i<N; i++) { /* 将原始序列逆序存入初始链表List */ 45 tmp = (PtrToNode)malloc(sizeof(struct Node)); 46 tmp->key = A[i]; 47 tmp->next = List; 48 List = tmp; 49 } 50 /* 下面开始排序 */ 51 for (D=1; D<=MaxDigit; D++) { /* 对数据的每一位循环处理 */ 52 /* 下面是分配的过程 */ 53 p = List; 54 while (p) { 55 Di = GetDigit(p->key, D); /* 获得当前元素的当前位数字 */ 56 /* 从List中摘除 */ 57 tmp = p; p = p->next; 58 /* 插入B[Di]号桶尾 */ 59 tmp->next = NULL; 60 if (B[Di].head == NULL) 61 B[Di].head = B[Di].tail = tmp; 62 else { 63 B[Di].tail->next = tmp; 64 B[Di].tail = tmp; 65 } 66 } 67 /* 下面是收集的过程 */ 68 List = NULL; 69 for (Di=Radix-1; Di>=0; Di--) { /* 将每个桶的元素顺序收集入List */ 70 if (B[Di].head) { /* 如果桶不为空 */ 71 /* 整桶插入List表头 */ 72 B[Di].tail->next = List; 73 List = B[Di].head; 74 B[Di].head = B[Di].tail = NULL; /* 清空桶 */ 75 } 76 } 77 } 78 /* 将List倒入A[]并释放空间 */ 79 for (i=0; i<N; i++) { 80 tmp = List; 81 List = List->next; 82 A[i] = tmp->key; 83 free(tmp); 84 } 85 } 86 87 int main() 88 { 89 int a[] = {34,8,64,51,32,21}; 90 LSDRadixSort(a, 6); 91 for(int i = 0; i < 6; i++) 92 printf("%d ",a[i]); 93 return 0; 94 }

1 #include <stdio.h> 2 #include <stdlib.h> 3 4 typedef int ElementType; 5 6 /* 基数排序 - 主位优先 */ 7 8 /* 假设元素最多有MaxDigit个关键字,基数全是同样的Radix */ 9 10 #define MaxDigit 4 11 #define Radix 10 12 13 /* 桶元素结点 */ 14 typedef struct Node *PtrToNode; 15 struct Node{ 16 int key; 17 PtrToNode next; 18 }; 19 20 /* 桶头结点 */ 21 struct HeadNode { 22 PtrToNode head, tail; 23 }; 24 typedef struct HeadNode Bucket[Radix]; 25 26 int GetDigit ( int X, int D ) 27 { /* 默认次位D=1, 主位D<=MaxDigit */ 28 int d, i; 29 30 for (i=1; i<=D; i++) { 31 d = X%Radix; 32 X /= Radix; 33 } 34 return d; 35 } 36 37 void MSD( ElementType A[], int L, int R, int D ) 38 { /* 核心递归函数: 对A[L]...A[R]的第D位数进行排序 */ 39 int Di, i, j; 40 Bucket B; 41 PtrToNode tmp, p, List = NULL; 42 if (D==0) return; /* 递归终止条件 */ 43 44 for (i=0; i<Radix; i++) /* 初始化每个桶为空链表 */ 45 B[i].head = B[i].tail = NULL; 46 for (i=L; i<=R; i++) { /* 将原始序列逆序存入初始链表List */ 47 tmp = (PtrToNode)malloc(sizeof(struct Node)); 48 tmp->key = A[i]; 49 tmp->next = List; 50 List = tmp; 51 } 52 /* 下面是分配的过程 */ 53 p = List; 54 while (p) { 55 Di = GetDigit(p->key, D); /* 获得当前元素的当前位数字 */ 56 /* 从List中摘除 */ 57 tmp = p; p = p->next; 58 /* 插入B[Di]号桶 */ 59 if (B[Di].head == NULL) B[Di].tail = tmp; 60 tmp->next = B[Di].head; 61 B[Di].head = tmp; 62 } 63 /* 下面是收集的过程 */ 64 i = j = L; /* i, j记录当前要处理的A[]的左右端下标 */ 65 for (Di=0; Di<Radix; Di++) { /* 对于每个桶 */ 66 if (B[Di].head) { /* 将非空的桶整桶倒入A[], 递归排序 */ 67 p = B[Di].head; 68 while (p) { 69 tmp = p; 70 p = p->next; 71 A[j++] = tmp->key; 72 free(tmp); 73 } 74 /* 递归对该桶数据排序, 位数减1 */ 75 MSD(A, i, j-1, D-1); 76 i = j; /* 为下一个桶对应的A[]左端 */ 77 } 78 } 79 } 80 81 void MSDRadixSort( ElementType A[], int N ) 82 { /* 统一接口 */ 83 MSD(A, 0, N-1, MaxDigit); 84 } 85 86 int main() 87 { 88 int a[] = {34,8,64,51,32,21}; 89 MSDRadixSort(a, 6); 90 for(int i = 0; i < 6; i++) 91 printf("%d ",a[i]); 92 return 0; 93 }
标签:
原文地址:http://www.cnblogs.com/kuotian/p/5469341.html