标签:
Isenbaev是国外的一个大牛。
现在有许多人要参加ACM ICPC。
一共有n个组,每组3个人。同组的3个人都是队友。
大家都想知道自己与大牛的最小距离是多少。
大牛与自己的最小距离当然是0。大牛的队友和大牛的最小距离是1。大牛的队友的队友和大牛的最小距离是2……以此类推。
如果实在和大牛没有关系的只好输出undefined了。
第一行读入n。表示有n个组。1 ≤ n ≤ 100
接下来n行,每行有3个名字,名字之间用空格隔开。每个名字的开头都是大写的。
每行输出一个名字,名字后面空格后输出数字a或者字符串undefined,a代表最小距离。
名字按字典序输出。
Sample Input
7
Isenbaev Oparin Toropov
Ayzenshteyn Oparin Samsonov
Ayzenshteyn Chevdar Samsonov
Fominykh Isenbaev Oparin
Dublennykh Fominykh Ivankov
Burmistrov Dublennykh Kurpilyanskiy
Cormen Leiserson Rivest
Sample Output
Ayzenshteyn 2
Burmistrov 3
Chevdar 3
Cormen undefined
Dublennykh 2
Fominykh 1
Isenbaev 0
Ivankov 2
Kurpilyanskiy 3
Leiserson undefined
Oparin 1
Rivest undefined
Samsonov 2
Toropov 1解决这个问题的方法就是使用广度优先搜索。所以我们先提出广度优先搜索的知识点分析。
知识点来自于:广度/宽度优先搜索(BFS)
广度优先搜索(也称宽度优先搜索,缩写BFS,以下采用广度来描述)是连通图的一种遍历策略。因为它的思想是从一个顶点V0开始,辐射状地优先遍历其周围较广的区域,故得名。
一般可以用它做什么呢?一个最直观经典的例子就是走迷宫,我们从起点开始,找出到终点的最短路程,很多最短路径算法就是基于广度优先的思想成立的。
算法导论里边会给出不少严格的证明,我想尽量写得通俗一点,因此采用一些直观的讲法来伪装成证明,关键的point能够帮你get到就好。
刚刚说的广度优先搜索是连通图的一种遍历策略,那就有必要将图先简单解释一下。
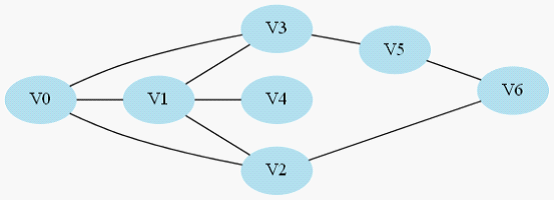
如图2-1所示,这就是我们所说的连通图,这里展示的是一个无向图,连通即每2个点都有至少一条路径相连,例如V0到V4的路径就是V0->V1->V4。
一般我们把顶点用V缩写,把边用E缩写。
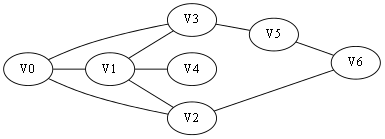
常常我们有这样一个问题,从一个起点开始要到一个终点,我们要找寻一条最短的路径,从图2-1举例,如果我们要求V0到V6的一条最短路(假设走一个节点按一步来算)【注意:此处你可以选择不看这段文字直接看图3-1】,我们明显看出这条路径就是V0->V2->V6,而不是V0->V3->V5->V6。先想想你自己刚刚是怎么找到这条路径的:首先看跟V0直接连接的节点V1、V2、V3,发现没有V6,进而再看刚刚V1、V2、V3的直接连接节点分别是:{V0、V4}、{V0、V1、V6}、{V0、V1、V5}(这里画删除线的意思是那些顶点在我们刚刚的搜索过程中已经找过了,我们不需要重新回头再看他们了)。这时候我们从V2的连通节点集中找到了V6,那说明我们找到了这条V0到V6的最短路径:V0->V2->V6,虽然你再进一步搜索V5的连接节点集合后会找到另一条路径V0->V3->V5->V6,但显然他不是最短路径。
你会看到这里有点像辐射形状的搜索方式,从一个节点,向其旁边节点传递病毒,就这样一层一层的传递辐射下去,知道目标节点被辐射中了,此时就已经找到了从起点到终点的路径。
我们采用示例图来说明这个过程,在搜索的过程中,初始所有节点是白色(代表了所有点都还没开始搜索),把起点V0标志成灰色(表示即将辐射V0),下一步搜索的时候,我们把所有的灰色节点访问一次,然后将其变成黑色(表示已经被辐射过了),进而再将他们所能到达的节点标志成灰色(因为那些节点是下一步搜索的目标点了),但是这里有个判断,就像刚刚的例子,当访问到V1节点的时候,它的下一个节点应该是V0和V4,但是V0已经在前面被染成黑色了,所以不会将它染灰色。这样持续下去,直到目标节点V6被染灰色,说明了下一步就到终点了,没必要再搜索(染色)其他节点了,此时可以结束搜索了,整个搜索就结束了。然后根据搜索过程,反过来把最短路径找出来,图3-1中把最终路径上的节点标志成绿色。
整个过程就如:


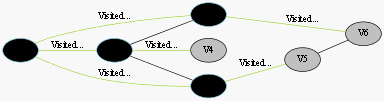
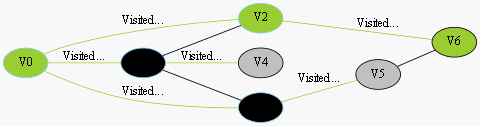
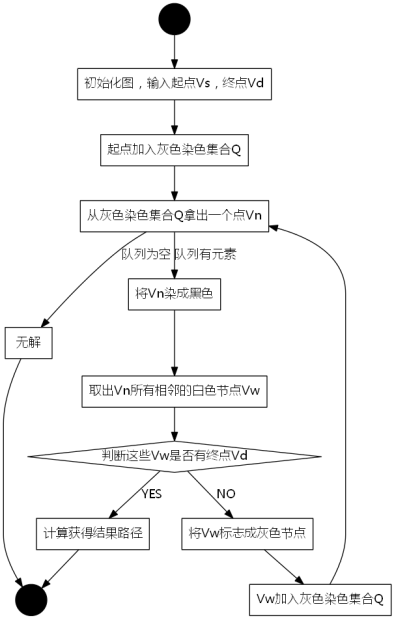
《迷宫问题》
定义一个二维数组:
int maze[5][5] = {
0, 1, 0, 0, 0,
0, 1, 0, 1, 0,
0, 0, 0, 0, 0,
0, 1, 1, 1, 0,
0, 0, 0, 1, 0,
};它表示一个迷宫,其中的1表示墙壁,0表示可以走的路,只能横着走或竖着走,不能斜着走,要求编程序找出从左上角到右下角的最短路线。
题目保证了输入是一定有解的。
也许你会问,这个跟广度优先搜索的图怎么对应起来?BFS的第一步就是要识别图的节点跟边!
节点就是某种状态,边就是节点与节点间的某种规则。
对应于《迷宫问题》,你可以这么认为,节点就是迷宫路上的每一个格子(非墙),走迷宫的时候,格子间的关系是什么呢?按照题目意思,我们只能横竖走,因此我们可以这样看,格子与它横竖方向上的格子是有连通关系的,只要这个格子跟另一个格子是连通的,那么两个格子节点间就有一条边。
如果说本题再修改成斜方向也可以走的话,那么就是格子跟周围8个格子都可以连通,于是一个节点就会有8条边(除了边界的节点)。
对应于题目的输入数组:
0, 1, 0, 0, 0,
0, 1, 0, 1, 0,
0, 0, 0, 0, 0,
0, 1, 1, 1, 0,
0, 0, 0, 1, 0,我们把节点定义为(x,y),(x,y)表示数组maze的项maze[x][y]。
于是起点就是(0,0),终点是(4,4)。按照刚刚的思路,我们大概手工梳理一遍:
初始条件:
起点Vs为(0,0)
终点Vd为(4,4)
灰色节点集合Q={}
初始化所有节点为白色节点
开始我们的广度搜索!
手工执行步骤【PS:你可以直接看图4-1】:
1.起始节点Vs变成灰色,加入队列Q,Q={(0,0)}
2.取出队列Q的头一个节点Vn,Vn={0,0},Q={}
3.把Vn={0,0}染成黑色,取出Vn所有相邻的白色节点{(1,0)}
4.不包含终点(4,4),染成灰色,加入队列Q,Q={(1,0)}
5.取出队列Q的头一个节点Vn,Vn={1,0},Q={}
6.把Vn={1,0}染成黑色,取出Vn所有相邻的白色节点{(2,0)}
7.不包含终点(4,4),染成灰色,加入队列Q,Q={(2,0)}
8.取出队列Q的头一个节点Vn,Vn={2,0},Q={}
9.把Vn={2,0}染成黑色,取出Vn所有相邻的白色节点{(2,1), (3,0)}
10.不包含终点(4,4),染成灰色,加入队列Q,Q={(2,1), (3,0)}
11.取出队列Q的头一个节点Vn,Vn={2,1},Q={(3,0)}
12. 把Vn={2,1}染成黑色,取出Vn所有相邻的白色节点{(2,2)}
13.不包含终点(4,4),染成灰色,加入队列Q,Q={(3,0), (2,2)}
14.持续下去,知道Vn的所有相邻的白色节点中包含了(4,4)……
15.此时获得了答案起始你很容易模仿上边过程走到终点,那为什么它就是最短的呢?
怎么保证呢?
我们来看看广度搜索的过程中节点的顺序情况:

你是否观察到了,广度搜索的顺序是什么样子的?
图中标号即为我们搜索过程中的顺序,我们观察到,这个搜索顺序是按照上图的层次关系来的,例如节点(0,0)在第1层,节点(1,0)在第2层,节点(2,0)在第3层,节点(2,1)和节点(3,0)在第3层。
我们的搜索顺序就是第一层->第二层->第三层->第N层这样子。
我们假设终点在第N层,因此我们搜索到的路径长度肯定是N,而且这个N一定是所求最短的。
我们用简单的反证法来证明:假设终点在第N层上边出现过,例如第M层,M
/**
* 广度优先搜索
* @param Vs 起点
* @param Vd 终点
*/
bool BFS(Node& Vs, Node& Vd){
queue<Node> Q;
Node Vn, Vw;
int i;
//初始状态将起点放进队列Q
Q.push(Vs);
hash(Vw) = true;//设置节点已经访问过了!
while (!Q.empty()){//队列不为空,继续搜索!
//取出队列的头Vn
Vn = Q.front();
//从队列中移除
Q.pop();
while(Vw = Vn通过某规则能够到达的节点){
if (Vw == Vd){//找到终点了!
//把路径记录,这里没给出解法
return true;//返回
}
if (isValid(Vw) && !visit[Vw]){
//Vw是一个合法的节点并且为白色节点
Q.push(Vw);//加入队列Q
hash(Vw) = true;//设置节点颜色
}
}
}
return false;//无解
} 对于这道题,首先我们把每个string名称绑定一个numeric编号,用来在一个数组里面存储他们相应的距离。节点就是map的first部分,边是同一个3维数组里面的各个string。
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<map>
#include<string>
#include<queue>
using namespace std;
map<string, int> hh;
map<string, int>::iterator it;
queue<int> que;
string str;
string s[110][4];
int dis[11000];
int main() {
str = "Isenbaev";
int n;
scanf("%d", &n);
int tot = 0; // tot实际上是每个名称的编号。
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= 3; j++) {
cin >> s[i][j];
if (hh.find(s[i][j]) == hh.end()) {
hh[s[i][j]] = ++tot;
}
}
}
bool flag = false;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= 3; j++) {
if (s[i][j] == str) {
flag = true;
break;
}
}
}
// 如果没有找到str就全部都为undefined
if (!flag) {
for (it = hh.begin(); it != hh.end(); it++)
cout << it->first << " undefined\n";
return 0;
}
while (!que.empty()) que.pop(); // 清空队列
que.push(hh[str]); // 把str的编号放入queue头部
memset(dis, -1, sizeof(dis)); // 把所有的dis设为-1
dis[hh[str]] = 0; // str的dis为0
while (!que.empty()) { // 当que为空时,说明已经结束搜索。
int x = que.front(); // 输出头部
que.pop();
for (int i = 1; i <= n; i++)
for (int j = 1; j <= 3; j++) {
int id = hh[s[i][j]]; // 为了找到头部编号的dis
if (id != x) continue;
for (int k = 1; k <= 3; k++) {
int num = hh[s[i][k]];
if (dis[num] == -1) {
dis[num] = dis[x]+1;
que.push(num);
}
}
}
}
for (it = hh.begin(); it != hh.end(); it++) {
cout << it->first << " ";
if (dis[it->second] == -1)
cout << "undefined" << "\n";
else
cout << dis[it->second] << "\n";
}
}标签:
原文地址:http://blog.csdn.net/stary_yan/article/details/51345501