标签：

七月算法-12月机器学习在线班--第十二次课笔记—支持向量机（SVM）

七月算法（julyedu.com）12月机器学习在线班学习笔记http://www.julyedu.com

?

复习的内容：

1. 对偶问题

   

2. KKT条件

   

   ?

SVM

1.1三类数据类型

1. 线性可分支持向量机
2. 线性支持向量机
3. 非线性支持向量机

?

1.2 线性分类

1.2.1 样本到分类面的距离的意义

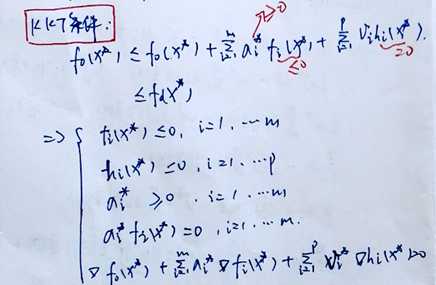
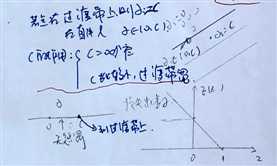
点到直线的距离，ABC是归一化的。"+"正类别，"-"负类别

因此距离可以直接用AX+BY+c=f(x,y)的函数值表示

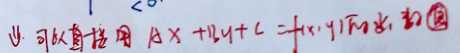
可以写成如下的向量形式：

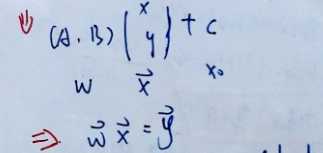
计算N个样本点到直线距离的最小值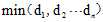，，之后在这些直线中知道到最大值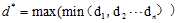

接下来就是计算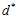

?

1.2.2 输入数据

1.2.3 线性可分支持向量机

如图，中3个支撑向量

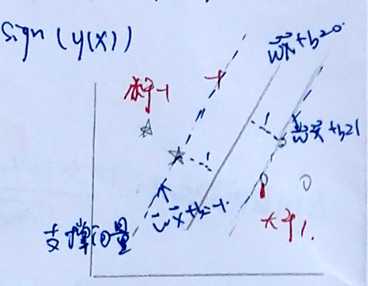
1，函数间隔和几何间隔：

,2， 最大间隔分离超平面

目标函数：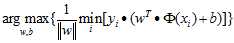

又因为目标函数中括号中的数全部大于等于1，即：

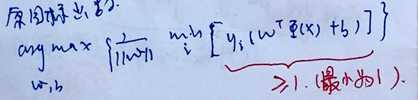
所以可以得到新的目标函数和其约束条件如下：

则，新的目标函数如下：

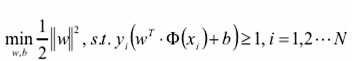
带不等式约束的凸优化的问题，用拉格朗日乘子法

1. 原问题是极小极大问题

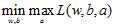
   转化成：原始问题的对偶问题，是极大极小问题：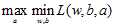

   拉格朗日乘子法

   

接下来就去L(w,b,a)的极大值，算法是SMO求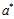的极大值

求的a=0,不是支撑向量，a是稀疏的，大多数的样本为0

1.3 线性支持向量机（数据线性不可分的）

1， 不一定分类完全正确的超平面就是最好的

2， 如果样本数据本身线性不可分

需要加入松弛因子（）：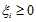

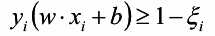
则目标函数就变为：

则带松弛因子的SVM拉格朗日函数

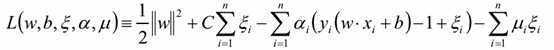
同样的可以得到对偶函数，转化成求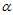的极值

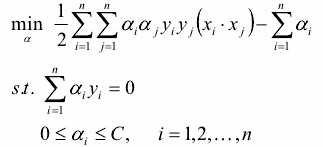
松弛因子已经被消了，最后求出最优解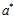，反带回去，求得W，b。

?

损失函数分析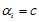：刚好没有惩罚

核函数：

可以使用核函数，将原始输入空间映射到新的特征空间，从而，使得原本线性不可分的样本可能在核空间可分。

高斯核函数RBF，是映射到无穷维度，（利用了泰勒展开），但是容易过拟合。

?

1.3 SVM中系数的求解：SMO（每次只选择两个乘子做）

1，有多个拉格朗日乘子

2，每次只选择其中两个乘子做优化，其他因子认为是常数。

?

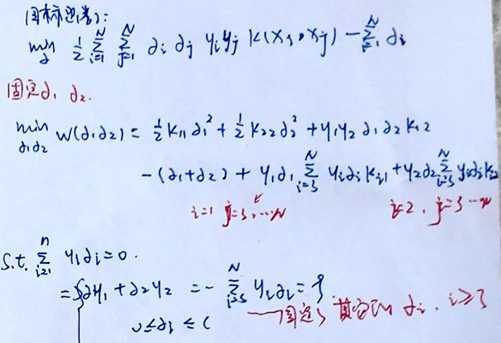
二变量优化问题

由上述可知，如果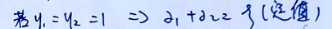则可得到如下的图：

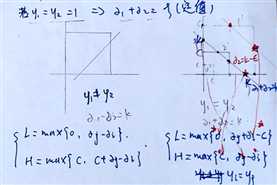
其中LH的对应关系，如图

程序退出的条件是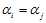：，也就是此时不更新权值了。

七月算法--12月机器学习在线班-第十二次课笔记—支持向量机（SVM）

标签：

原文地址：http://www.cnblogs.com/sweet-dew/p/5488053.html