标签:
七月算法(julyedu.com)12月机器学习在线班学习笔记http://www.julyedu.com
?
EM Expection Maxium 期望最大化
1 引例
1000人,统计身高,1.75,1.62,1.94,有多少男女,每个身高对应的男女
?
1.1 如何算?利用极大似然估计,估算均值和方差

上述结论和矩估计的结果是一致的,
即:样本的均值即高斯分布的均值,样本的伪方差即高斯分布的方差。
如果是高斯分布,就可以这么用本计算,均值和方差
?
设定,男女的身高服从两个高斯分布

随机变量X是有K个高斯分布混合而成,若观测到随机变量X的一系列样本x1,x2,...,xn,
则目标函数为:对数似然函数
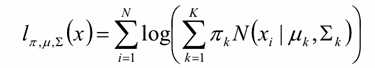
由于在对数函数里面又有加和,没法直接用求导解方程的办法直接求得极大值。分成两步
?
1.2 直观上的理解EM
STEP1: 估算数据来自哪个组份

STEP2: 估计每个组份的参数
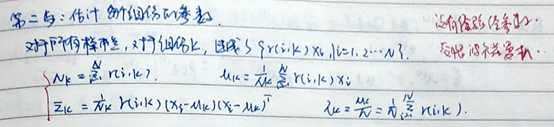
1.3 高斯式证明

有上图的图中可以得知:做期望的极大,不停的做期望的极大
?
利用Jensen不等式(凸优化可以直接用)
令Qi是z的某一个分布,Qi≥0,有:

进一步分析:有上面的等式成立可以得知,p,q成正比;
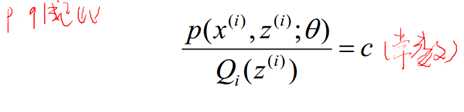
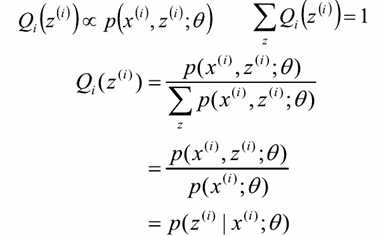
则可以得到EM的整体框架图

?
1.4 从理论公式推导GMM
随机变量X是有K个高斯分布混合而成取各个高斯分布的概率为φ1φ2... φK,第i个高斯分布的均值为μi,方差为Σi。若观测到随机变量X的一系列样本x1,x2,...,xn,试估计参数π,μ,Σ。
分别是E-STEP,和M-step
E-STEP:

M-step:(先写出期望,在求极大值)
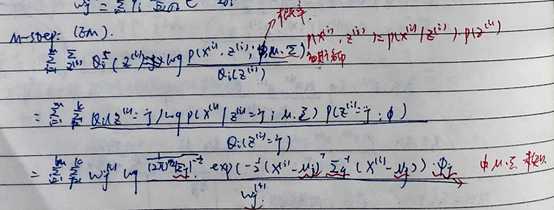
对均值求偏导,令上式等于0,解的均值:

同理,可以得到方差的值。
在得到方差和均值后,对φ求偏导,约束条件是φ1+φ2+... φK=1,也就是带等式的约束条件求极值,拉格朗日乘子法
最终得到的式子和,最原先开始欧拉式的解释一样
对于所有的数据点,可以看作组份k生成了这些点。组份k是一个标准的高斯分布
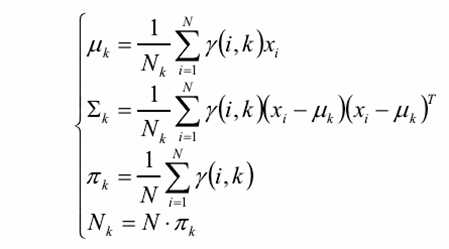
带有隐变量的方法:EM+变分
?
标签:
原文地址:http://www.cnblogs.com/sweet-dew/p/5488049.html