标签：

七月算法-12月机器学习--第十五次课笔记—主题模型

七月算法（julyedu.com）12月机器学习在线班学习笔记http://www.julyedu.com

复习的知识：

1.，Γ函数

是阶乘在实数上的推广，即实数的阶乘

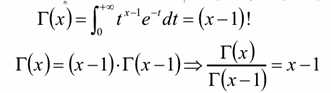
2，Beta分布

Beta分布的概率密度：

其中系数B为：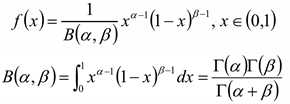

两者的关系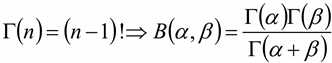

1，朴素贝叶斯分析

     朴素贝叶斯没有分析语意，无法解决语料中一词多义和多词一义的问题，更像是词法的分析，可以 

      一， 1个词可能被映射到多个主题中——一词多义

      二，多个词可能被映射到某个主题的概率很高——多词一义

2 pLSA模型（推导）    

带有隐变量的首先想到的是EM算法

2.1 记号

文档到主题之间是多项分布，主题到词也是多项分布，生成模型，head-to-tail, 计算每一篇文档的主题是什么分布，（隐变量）

head-to-tail模型，所以可以得到

2.2极大似然估计：在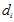中出现的次数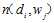

所有文档的所有词做乘积，后面的乘积计算和以前的抛硬币是相同的例子

未知的变量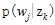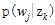， ，使用EM算法，两步走

第一步：求隐含变量主题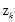的后验概率

第二步：似然函数期望求极大

• 先求似然函数

• 再求条件分布的期望

将隐变量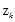暴露出来

• 带等式约束的求极值问题，使用Lagrange乘子法解决。

2.3 总结

1. pLSA可以看做概率化的矩阵分解，没有直接做矩阵分解。

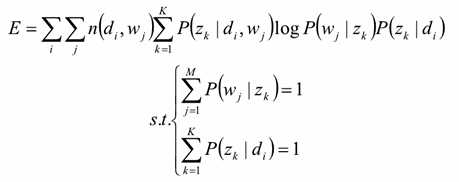
     2，不需要先验信息，可完成学习

3 LDA模型

3.1 Dirichlet分布

   2元到K元

  从2到K： 二项分布到多项分布， Beta分布到Dirichlet分布

  P有K-1个参数，而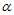是K个参数

3.2 LDA的解释

     1. 共有m篇文章，一共涉及了K个主题；

    2，每篇文章(长度为Nm)都有各自的主题分布，主题分布是多项分布，该多项分布的参数服从Dirichlet分布，该Dirichlet分布的参数为α；

    3，每个主题都有各自的词分布，词分布为多项分布，该多项分布的参数服从Dirichlet分布，该Dirichlet分布的参数为β；

解释如下图

3.3 参数的学习

给定一个文档集合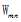，是可以观察到的已知变量，α和β是根据经验给定的先验参数，其他的变量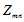、θ、φ都是未知的隐含变量

则似然概率为：

4 Gibbs 采样（Gibbs Sampling）

Gibbs Sampling算法的运行方式是每次选取概率向量的一个维度，给定其他维度的变量值采样当前维度的值。不断迭代直到收敛输出待估计的参数。

4.1 Gibbs更新规则

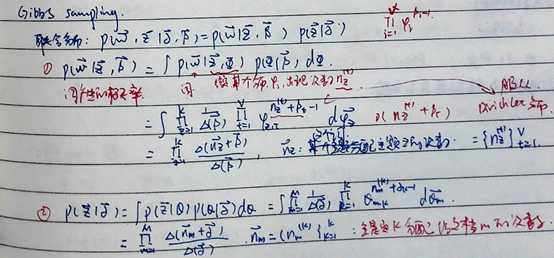
最后得到的就是编码所需要的公式

总结：坐标上升，给定K个参数，先固定几个，不停的迭代，SMO/EM/Gibbs/变分

4.2 代码实现

三个矩阵和三个向量

z[d][w] ：第d篇文档的第w个词来自哪个主题。M行，X列，X为相应文档长度：即词(可重复)的数目。

nw[w][t]：第w个词是第t个主题的次数。word-topic矩阵，列向量nw[][t]表示主题t的词频数分布；V行K列

nd[d][t]：第d篇文档中第t个主题出现的次数，doc-topic矩阵，行向量nd[d]表示文档d的主题频数分布。M行，K列。

4.3超参数的确定

1，交叉验证,

2，α=50/K

5 LDA总结

1. LDA用于短文档往往效果不明显
2. LDA可以和其他算法相结合。

   使用LDA将长度为Ni的文档降维到K维(主题的数目)，同时给出每个主题的概率(主题分布)

七月算法-12月机器学习在线班--第十五次课笔记—主题模型

标签：

原文地址：http://www.cnblogs.com/sweet-dew/p/5490877.html