标签：

七月算法-12月机器学习--第十六次课笔记—采样和变分

七月算法（julyedu.com）12月机器学习在线班学习笔记http://www.julyedu.com

第一部分 采样

引言

为什么要研究采样？

根据采样结果估算分布的参数，完成参数学习。

前提：模型已经存在，但参数未知；

方法：通过采样的方式，获得一定数量的样本，从而学习该系统的参数。

1 采样算法

现需要对概率密度函数f(x)的参数进行估计，若已知的某概率密度函数g(x)容易采样获得其样本，可以如何估计f(x)的参数？

g(x)很容易获取样本，譬如，高斯，均匀分布等等，用简单地分布g(x)来估计f(x)

1.1 带拒绝采样

1.2 Matropolis-Hastings算法

A, 算法的模型

B，分析MH率

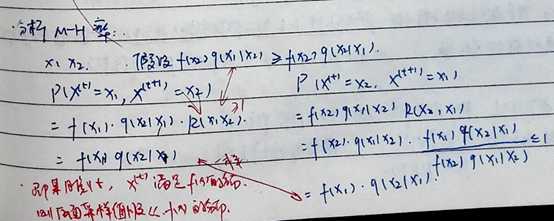
下面证明以上的结论

1.3马尔科夫随机过程的平稳分布（MCMC）    

1.3.1 基本的知识

初始概率不同，但经过若干次迭代， π最终稳定收敛在某个分布上。

下面两种写法等价：    

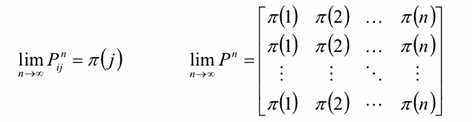
则矩阵A行加和为1，则一定结果可以满足全1向量，如上图，则可以判断，（1,1……，1）是A的特征向量，1是A的特征值，

对于某概率分布π，生成一个能够收敛到概率分布π的马尔科夫状态转移矩阵P，则经过有限次迭代，一定可以得到概率分布π。

使用MCMC算法模拟 (Markov Chain Monte Carlo)。

1.3.2 细致平稳条件

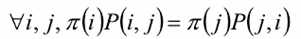
则π(x)是马尔科夫过程的平稳分布。上式又被称作细致平稳条件(detailed balance condition) 。

细节上面是稳态的

1.3.4 细致平稳条件和平稳分布的关系

1.3.5 设定接受率（小于1的一个数）

对于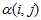取小于1的数，因为接受率要小于1，即：

1.4 改造的MCMC算法

MCMC有一定的拒绝率。

基于以上的结论，可以得到：二维Gibbs采样算法：

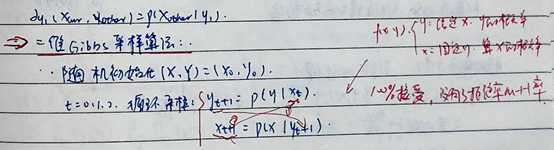
由以上的结论可以看出M-H拒绝率没有， 也就是百分之一百接受

可以推广到高维

固定邻居的值，当前的值

总结：可以用采样改造EM算法

第二部分 变分

2.1 变分的核心

2.2 变分的推导

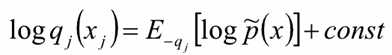
变分推导(variational inference)是一般的确定性的近似推导算法。

思路：选择一个容易计算的近似分布q(x)，它能够尽可能的接近真正的后验分布p(x|D)。

用什么的相似度呢？KL散度

2.2.1 近似分布的KL散度

KL散度至少可以找到一个局部分极值

2.2.2 新目标函数

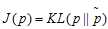
由上图可以得出：

1, 因为KL散度总是非负的，J(p)是NLL的上界

2, 因此，L(q)是似然函数的下界，当q=p*时取等号。 可取等号，说明下界是紧的(tight)

变分的目的是为了求参数

2.3 变分和EM的联系

EM算法：计算关于隐变量后验概率的期望，得到下界；

变分：计算KL散度，得到下界；

相同的思维：不断迭代，得到更好的下界，不断上升。

2.4 平均场方法(Mean field method)

N个因子的乘积

变分的近似推导，主要的近似就在于这部分，即：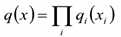

2.5 变分的推导

变分的总结：

变分既能够推断隐变量，也能推断未知参数。其难点在于公式演算略复杂。

和采样相对：一个容易计算但速度慢，一个不容易计算但运行效率高。

七月算法-12月机器学习在线班--第十六次课笔记—采样和变分

标签：

原文地址：http://www.cnblogs.com/sweet-dew/p/5490900.html