标签：
七月算法（julyedu.com）12月机器学习在线班学习笔记http://www.julyedu.com
?
随机森林：多棵树，对当前节点做划分是最重要的
决策树学习采用的是自顶向下的递归方法，其基本思想是以信息熵为度量构造一棵熵值下降最快的树
叶子节点处的熵值为零，此时每个叶节点中的实例都属于同一类。
?
下面的重点是选择什么样的熵值下降最快
建立决策树的关键，即在当前状态下选择哪个属性作为分类依据。
根据不同的目标函数，建立决策树主要有以下下三种算法
ID3 C4.5 CART，三种学习思路一样
1，概念：所对应的熵和条件熵分别称为经验熵和经验条件熵。
信息增益：表示得知特征A的信息而使得类X的信息的不确定性减少的程度。
定义：特征A对训练数据集D的信息增益g(D,A)，定义为集合D的经验熵H(D)与特征A给定条件下D的经验条件熵H(D|A)之差，即：
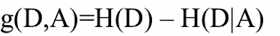
本质上是计算H(D)，H(D|A)
2，基本记号
3，信息增益的计算方法
计算数据集D的经验熵
?
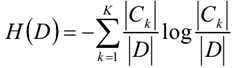
遍历所有特征，对于特征A：
计算特征A对数据集D的经验条件熵H(D|A)
计算特征A的信息增益：g(D,A)=H(D) – H(D|A)
H(D|A)的计算方法如下：
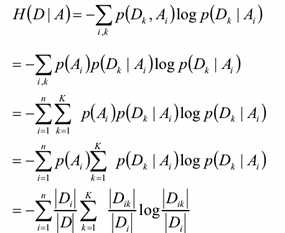
选择信息增益最大的特征作为当前的分裂特征，以此计算每个特征选择最大的那个
信息增益率：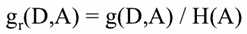
Gini系数:
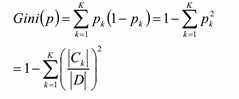
关于Gini系数的讨论
Gini系数的第二定义
一个属性的信息增益(率)/gini指数越大，表明属性对样本的熵减少的能力更强，这个属性使得数据由不确定性变成确定性的能力越强。
决策树对训练属于有很好的分类能力，但对未知的测试数据未必有好的分类能力，泛化能力弱，即可能发生过拟合现象。
剪枝和随机森林的手段防止过拟合
A, Bagging的策略（加了一个随机采样）
1，bootstrap aggregation
2，从样本集中重采样(有重复的)选出n个样本
3，在所有属性上，对这n个样本建立分类器(ID3、C4.5、CART、SVM、Logistic回归
4，重复以上两步m次，即获得了m个分类器? 将数据放在这m个分类器上，
5，最后根据这m个分类器的投票结果，决定数据属于哪一类
B, 随机森林
和Bagging的策略不同的是：（不在所有的属性上做，相当于增加了随机性）
1，从样本集中用Bootstrap采样选出n个样本；
2，从所有属性中随机选择k个属性，选择最佳分割属性作为节点建立CART决策树；
3，重复以上两步m次，即建立了m棵CART决策树
4，这m个CART形成随机森林，通过投票表决结果，决定数据属于哪一类
一种可能的方案
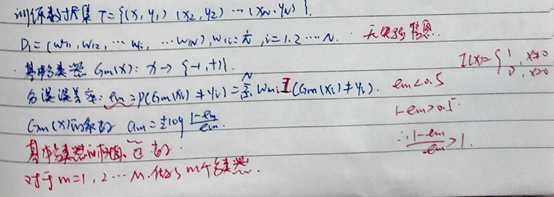
其中最关键的是Gm(X)的系数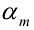
,以及需要注意的点：
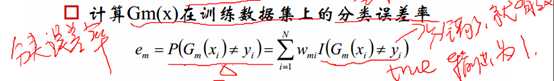
对于m=1,2,…M，做了M个分类器
A, 更新训练数据集的权值分布
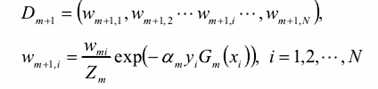
Zm是规范化因子
B,构建基本分类器的线性组合
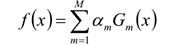
C, 得到最终分类器
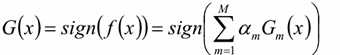
若这一次分类错误，则下一次，权值会提升，若分类正确则权值会下降
七月算法--12月机器学习在线班-第十一次课笔记—随机森林和提升
标签：
原文地址：http://www.cnblogs.com/sweet-dew/p/5490964.html
