标签：

1 最小二乘法概述

自从开始做毕设以来，发现自己无时无刻不在接触最小二乘法。从求解线性透视图中的消失点，m元n次函数的拟合，包括后来学到的神经网络，其思想归根结底全都是最小二乘法。

1-1 “多线→一点”视角与“多点→一线”视角

最小二乘法非常简单，我把它分成两种视角描述：

（1）已知多条近似交汇于同一个点的直线，想求解出一个近似交点：寻找到一个距离所有直线距离平方和最小的点，该点即最小二乘解；

（2）已知多个近似分布于同一直线上的点，想拟合出一个直线方程：设该直线方程为y=kx+b，调整参数k和b，使得所有点到该直线的距离平方之和最小，设此时满足要求的k=k0，b=b0，则直线方程为y=k0x+b0。

1-2 思维拓展

这只是举了两个简单的例子，其实在现实生活中我们可以利用最小二乘法解决更为复杂的问题。比方说有一个未知系数的二元二次函数f(x,y)=w0x^2+w1y^2+w2xy+w3x+w4y+w5，这里w0~w5为未知的参数，为了确定下来这些参数，将会给定一些样本点(xi,yi,f(xi,yi))，然后通过调整这些参数，找到这样一组w0~w5，使得这些所有的样本点距离函数f(x,y)的距离平方之和最小。至于具体用何种方法来调整这些参数呢？有一种非常普遍的方法叫“梯度下降法”，它可以保证每一步调整参数，都使得f(x,y)朝比当前值更小的方向走，只要步长α选取合适，我们就可以达成这种目的。

而这里不得不提的就是神经网络了。神经网络其实就是不断调整权值w和偏置b，来使得cost函数最小，从这个意义上来讲它还是属于最小二乘法。更为可爱的一点是，神经网络的调参用到的仍是梯度下降法，其中最常用的当属随机梯度下降法。而后面伟大的bp算法，其实就是为了给梯度下降法做个铺垫而已，bp算法的结果是cost函数对全部权值和全部偏置的偏导，而得知了这些偏导，对于各个权值w和偏置b该走向何方就指明了方向。

因此，最小二乘法在某种程度上无异于机器学习中基础中的基础，且具有相当重要的地位。至于上面所说的“梯度下降法”以及“利用最小二乘法求解二元二次函数的w0~w5”，我将会在后面的博客中进行更加详细的探讨。

2 scipy库中的leastsq函数

当然，最小二乘法本身实现起来也是不难的，就如我们上面所说的不断调整参数，然后令误差函数Err不断减小就行了。我们将在下一次博客中详细说明如何利用梯度下降法来完成这个目标。

而在本篇博客中，我们介绍一个scipy库中的函数，叫leastsq，它可以省去中间那些具体的求解步骤，只需要输入一系列样本点，给出待求函数的基本形状（如我刚才所说，二元二次函数就是一种形状——f(x,y)=w0x^2+w1y^2+w2xy+w3x+w4y+w5，在形状给定后，我们只需要求解相应的系数w0~w6），即可得到相应的参数。至于中间到底是怎么求的，这一部分内容就像一个黑箱一样。

2-1 函数形为y=kx+b

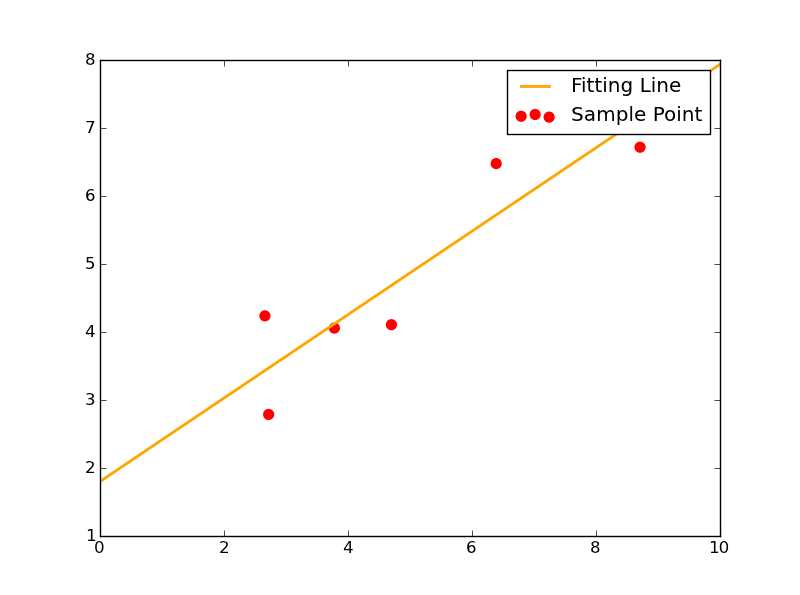
这一次我们给出函数形y=kx+b。这种情况下，待确定的参数只有两个：k和b。

此时给出7个样本点如下：

1 Xi=np.array([8.19,2.72,6.39,8.71,4.7,2.66,3.78])
2 Yi=np.array([7.01,2.78,6.47,6.71,4.1,4.23,4.05])

则使用leastsq函数求解其拟合直线的代码如下：

 1 ###最小二乘法试验###
 2 import numpy as np
 3 from scipy.optimize import leastsq
 4 
 5 ###采样点(Xi,Yi)###
 6 Xi=np.array([8.19,2.72,6.39,8.71,4.7,2.66,3.78])
 7 Yi=np.array([7.01,2.78,6.47,6.71,4.1,4.23,4.05])
 8 
 9 ###需要拟合的函数func及误差error###
10 def func(p,x):
11     k,b=p
12     return k*x+b
13 
14 def error(p,x,y,s):
15     print s
16     return func(p,x)-y #x、y都是列表，故返回值也是个列表
17 
18 #TEST
19 p0=[100,2]
20 #print( error(p0,Xi,Yi) )
21 
22 ###主函数从此开始###
23 s="Test the number of iteration" #试验最小二乘法函数leastsq得调用几次error函数才能找到使得均方误差之和最小的k、b
24 Para=leastsq(error,p0,args=(Xi,Yi,s)) #把error函数中除了p以外的参数打包到args中
25 k,b=Para[0]
26 print"k=",k,‘\n‘,"b=",b
27 
28 ###绘图，看拟合效果###
29 import matplotlib.pyplot as plt
30 
31 plt.figure(figsize=(8,6))
32 plt.scatter(Xi,Yi,color="red",label="Sample Point",linewidth=3) #画样本点
33 x=np.linspace(0,10,1000)
34 y=k*x+b
35 plt.plot(x,y,color="orange",label="Fitting Line",linewidth=2) #画拟合直线
36 plt.legend()
37 plt.show()

我把里面需要注意的点提点如下：

1、p0里放的是k、b的初始值，这个值可以随意指定。往后随着迭代次数增加，k、b将会不断变化，使得error函数的值越来越小。

2、func函数里指出了待拟合函数的函数形状。

3、error函数为误差函数，我们的目标就是不断调整k和b使得error不断减小。这里的error函数和神经网络中常说的cost函数实际上是一回事，只不过这里更简单些而已。

4、必须注意一点，传入leastsq函数的参数可以有多个，但必须把参数的初始值p0和其它参数分开放。其它参数应打包到args中。

5、leastsq的返回值是一个tuple，它里面有两个元素，第一个元素是k、b的求解结果，第二个元素我暂时也不知道是什么意思，先留下来。

其拟合效果图如下：

2-2 函数形为y=ax^2+bx+c

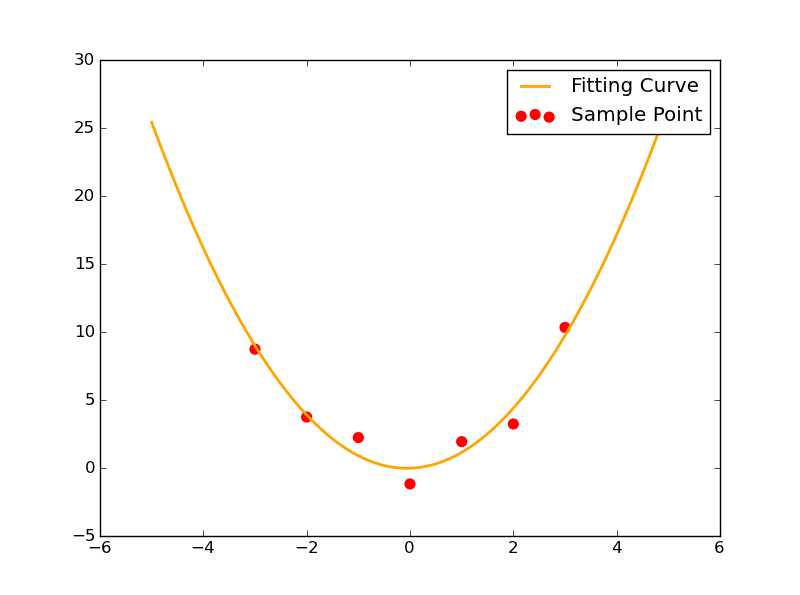
这一次我们给出函数形y=ax^2+bx+c。这种情况下，待确定的参数有3个：a，b和c。

此时给出7个样本点如下：

1 Xi=np.array([0,1,2,3,-1,-2,-3])
2 Yi=np.array([-1.21,1.9,3.2,10.3,2.2,3.71,8.7])

这一次的代码与2-1差不多，除了把待求参数再增加一个，换了一下训练样本，换了一下func中给出的函数形，几乎没有任何变化。

 1 ###最小二乘法试验###
 2 import numpy as np
 3 from scipy.optimize import leastsq
 4 
 5 ###采样点(Xi,Yi)###
 6 Xi=np.array([0,1,2,3,-1,-2,-3])
 7 Yi=np.array([-1.21,1.9,3.2,10.3,2.2,3.71,8.7])
 8 
 9 ###需要拟合的函数func及误差error###
10 def func(p,x):
11     a,b,c=p
12     return a*x**2+b*x+c
13 
14 def error(p,x,y,s):
15     print s
16     return func(p,x)-y #x、y都是列表，故返回值也是个列表
17 
18 #TEST
19 p0=[5,2,10]
20 #print( error(p0,Xi,Yi) )
21 
22 ###主函数从此开始###
23 s="Test the number of iteration" #试验最小二乘法函数leastsq得调用几次error函数才能找到使得均方误差之和最小的a~c
24 Para=leastsq(error,p0,args=(Xi,Yi,s)) #把error函数中除了p以外的参数打包到args中
25 a,b,c=Para[0]
26 print"a=",a,‘\n‘,"b=",b,"c=",c
27 
28 ###绘图，看拟合效果###
29 import matplotlib.pyplot as plt
30 
31 plt.figure(figsize=(8,6))
32 plt.scatter(Xi,Yi,color="red",label="Sample Point",linewidth=3) #画样本点
33 x=np.linspace(-5,5,1000)
34 y=a*x**2+b*x+c
35 plt.plot(x,y,color="orange",label="Fitting Curve",linewidth=2) #画拟合曲线
36 plt.legend()
37 plt.show()

不过我们发现，它依旧能够非常顺利地解出待求的三个参数。其拟合情况如图所示：

2-3 结语

本次博客给出了最小二乘法的Python实现方法，它用到了scipy库中的leastsq函数。在上面我们给出了两个实例，分别实现了对一元一次函数的拟合和一元二次函数的拟合，而事实上，对于函数并不一定得是一元函数，对于更多元的函数也同样能够利用最小二乘法完成拟合工作，不过随着元和次的增加，待求参数也就越来越多了，比方说二元二次函数就有6个待求参数w0~w6。

然为了更好地理解神经网络的训练算法，并不建议直接使用leastsq函数完成对未知参数的求解，因此在以后的博客中我会详细说明如何利用梯度下降法来求解误差函数的最小值。

3 下面要写的博客

1、梯度下降法（什么是梯度下降法，如何使用梯度下降法求一元二次函数最小值）

2、利用梯度下降法拟合二元二次函数（即求解w0~w5，相当于对梯度下降法的一个应用）

3、最小二乘法求解机器学习中cost函数最小值（什么是cost函数，并利用leastsq求解误差函数最小值）

2016.5.14

by 悠望南山

Python闲谈（二）聊聊最小二乘法以及leastsq函数

标签：

原文地址：http://www.cnblogs.com/NanShan2016/p/5493429.html