标签:
一般说的堆都是二叉堆。
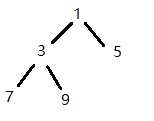
1. 首先,需要创建一个堆,二叉堆在结构上的特殊性(完全二叉树),使得我们可以用一个一维数组来保存它。例如:
这个堆就可以用 { 1, 3, 5, 7, 9 }来保存。那么在这个数据结构中,如何找到一个节点的两个子节点或者父节点呢?
只要用这个公式就可以了。父节点 = ( i - 1 )/2 ,子节点 = i * 2 + 1以及 i*2 + 2。
2. 创建堆需要的两个主要操作函数: 上滤,下滤。
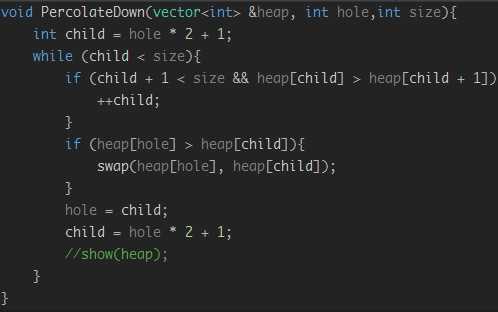
a. 下滤(percolate down):删除堆的第一个元素之后的恢复和创建堆时均用到了下滤操作。
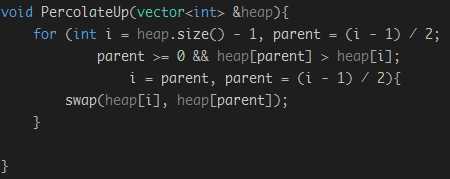
b. 上滤(percolate up):插入元素到堆中时用到了上滤操作。
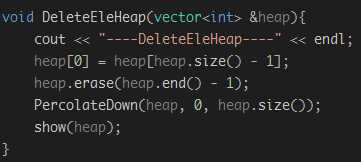
3. 删除:当删除堆头的元素时,堆中产生了一个空位,将数组中的最后一个元素交换到堆头,此时数组不满足堆序,需要对其进行下滤操作,即,将这个元素与两个子节点进行比较,与两个子节点中较大的进行交换,重复进行这个操作,将这个元素放到合适的位置,此时,该数组又满足了堆序。
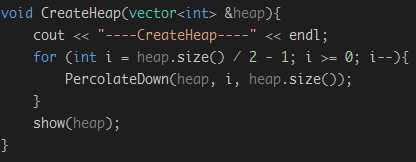
4. 创建:给定一个任意的数组,从最后一个父节点(size/2-1)开始,逐个进行下滤操作,当到达第一个父节点时,数组及变成了堆。
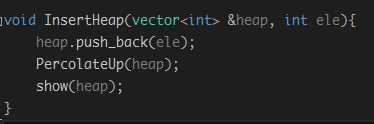
5. 插入:插入一个元素到堆中,将该元素插入到数组最后,对其进行上滤操作,即,将这个元素与父节点进行比较,若比父节点小则与父节点交换,重复进行这个操作,将这个元素放到合适的位置,插入操作结束。
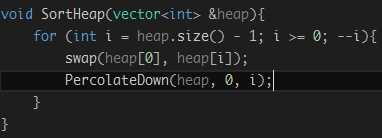
6. 排序:只要掌握了创建堆的几个主要操作,堆排序就很简单了。堆排序实际上是通过堆的特性,将堆头元素交换到数组的末尾,此时数组最后一个就是最小的元素,将剩下的n-1个数执行下滤操作,恢复堆序,重复上述操作,每次将最小的数放到数组末尾的有序数组之前,再对前边的数进行下滤操作,最后整个数组变成一个有序的数组。
值得一提的是:大顶堆执行排序后的数组是递增的,而小顶堆执行排序后的数组是递减的。
堆排序
标签:
原文地址:http://www.cnblogs.com/macher/p/5497742.html