标签:

写前面
webgl还真是个蛮麻烦的东西 相比普通2d绘图痛苦很多
如果你觉得canvas2d原生api已经足够你折腾了 那么webgl会让你更加手足无措~
难就难在webgl的绘制流程 因为它只提供了操作显卡的接口
webgl又像是opengl的妹妹一样 姐姐是面向过程的 那么妹妹也一样了!
 (我就是妹妹)
(我就是妹妹)
为此一大堆的流程全都丢给我们了。。。不封装直接使用还真是麻烦到爆炸
所以 之后原生api玩6后 肯定会封装一下以便使用的
--------------------------------------------------------------------这是webgl的第一篇 我该放上什么demo呢?
因为每次到了地铁后半段肚子都会及饿 都会想吃点什么 换成地铁的地方有个面包店 人气还挺好的 不过我吃来吃去就两样。。
一个是类似三明治的面包(三棱柱) 还有一个 是甜甜圈(环面) 前几天我就选择这两样最为此篇的demo了
三棱柱有点so easy了 所以我选择绘制甜甜圈作为第一篇webgl的东西
gif如下
也可以戳这个demo 请用chrome打开
那么怎么把环面的坐标表示出来呢?
我们可以先在 某个平面内表示个二维的圆 然后围绕一个轴转个一周 这就可以表示出来了
如图
现在xy平面内画个圆 然后围绕y轴 以r为半径转个一周
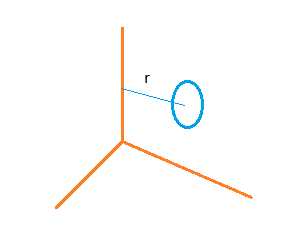
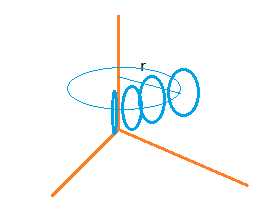
这就可以把甜甜圆的顶点坐标方程表示出来
接下来我们还得知道法向量 你看demo中是有光照效果的
法向量其实就是 横截面圆上每个点的向量坐标减去它圆心的向量
如下图 这个平面圆中其中某点的法向量
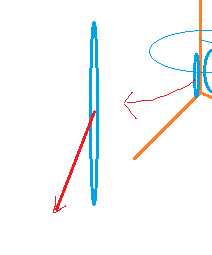
部分代码
const SweetRing = function(prop){ var [position,normal,color]=[[],[],[]]; var len; const [PI2,sin,cos] = [Math.PI*2,Math.sin,Math.cos]; const [r,g,b] = [247/255,182/255,99/255]; const {r1,r2,the_num,phe_num} = prop; const posf = (i,j)=>{ const [n1,n2] = [i/phe_num*PI2,j/the_num*PI2]; const xx = cos(n2)*r2+r1; const y = sin(n2)*r2; const [x,z] = [cos(n1)*xx,sin(n1)*xx]; const [nx,ny,nz] = [ x-cos(n1)*r1,y, z-sin(n1)*r1 ]; position.push(x,y,z); color.push(r,g,b ); normal.push(nx,ny,nz); }; for(let i = 0;i<=phe_num;++i){ for(let j = 0;j<=the_num;++j){ posf(i,j),posf(i+1,j),posf(i,j+1), posf(i+1,j+1),posf(i+1,j),posf(i,j+1); } } len = position.length/3; return{position,normal,color,len} }({ r1:2,r2:.8,the_num:36,phe_num:36 });
r1 r2 是两个半径 the_num phe_num 控制遍历顶点的数量
position 是坐标顶点
color是颜色顶点 这里每个顶点的rgb成分都相同
normal是法向量
可以看到一次内层循环中要执行4个posf函数 为什么呢?
因为我们的图元是三角 最终都是用三角表示出这个甜甜圈的
这4个posf表示出2个三角 他们的坐标关系就是(i,j) (i+1,j)(i,j+1)(i+1,j+1)(i+1,j)
接下来是着色器部分的代码 如下
gl.shaderSource(vs, ` attribute vec3 pos; attribute vec3 normal; attribute vec3 color; uniform mat4 pro; uniform mat4 mov; uniform mat4 rot; uniform mat4 rot2; uniform vec3 light1; uniform vec3 light2; varying vec3 co; void main(){ gl_Position = pro*mov*rot*rot2*vec4(pos , 1); vec3 n =(mov*rot*rot2*vec4(normalize(normal),0.0)).xyz; float nn = max(dot(n,normalize(vec3(0,.3,1))),0.0); co = nn*light1*color+light2; } `); gl.shaderSource(fs , ` precision highp float; varying lowp vec3 co; void main(){ gl_FragColor = vec4(co , 1); } `);
主要看光照那部分吧
这里运用到了两种光 分别是 环境光(light2)和平行光(light1) (其余光照以后探讨)
先讲平行光
平行光解决的就是 光线向量与物体的的某个法向量关系 得到光线对那个面的强度是怎样的
float nn = max(dot(n,normalize(vec3(0,.3,1))),0.0);
上面这行就是计算出法线与光线向量(0,.3,1)的点乘
记得对法线归一化 不然会对你提示警告 ‘index of range‘ (我当初就纳闷了。。。)
点乘的结果(nn) 分别于与平行光颜色和顶点颜色相乘 就得到混合的结果了
最后 再加上环境光就全部完成了
co = nn*light1*color+light2;
标签:
原文地址:http://www.cnblogs.com/daidaidai/p/5499791.html