标签:
目前通常使用的Haar-like特征主要包括Paul Viola和Michal Jones在人脸检测中使用的由Papageorgiou C首先提出的原始矩形特征和Rainer Lienhart 和 Jochen Maydt提出的扩展矩形特征。
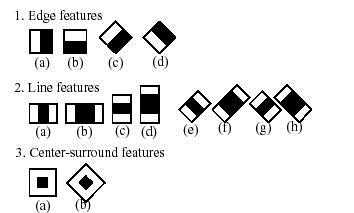
图1.Haar-like特征
Haar-like特征值的计算就是用图中矩形模板中黑色矩形内所有像素值的和减去白色矩形内所有像素值的和。Haar-like特征可以有效的提取图像的纹理特征,各模板通过平移、缩放提取不同位置和尺度的特征值。所以Haar-like特征的数量是巨大的,对于给定的W×H的图片,其一个矩形特征的数量为:
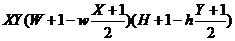
其中,wxh为特征模板尺寸
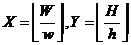
表示特征模板在水平和垂直方向放大的最大比例。而对于45度的特征数量为:
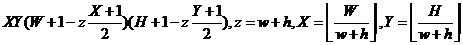
关于这个公式,其推导过程比较难懂。在此说说我的理解:
首先得清楚两点:
1、对于图2中的某一特征,特征本身可以沿水平、竖直方向缩放;水平方向需以w为单位缩放,竖直方向需以h为单位进行缩放;即缩放后宽高比可能与原特征宽高比不同,但缩放后,宽和高与原特征的宽和高是成比例的。所以对于图2中某一w*h的矩形,其有X*Y种放大方式。
2、对图2中的某一特征矩形及其缩放后的特征矩形,其处于图像的位置不同,Haar特征不同,所以需在窗口中滑动计算。例如图2中的1(a)特征大小为2*1,对于24*24的图像,水平可滑动23步,垂直可滑动24步,所以共有23*24个特征。
理解了这两点后如何绕开原著一大堆推导过程得到上述公式呢?
在此引用一个网友的相比之下简洁明了的推导过程:
这个公式是从概率方面得到的,因为haar特征框没有对宽和高做比例的限制,因此其两边个数的选择为独立同分布事件(此块不知如何用语言描述,如不能理解请直接看计算步骤)。因此以高度边为例,haar特征框为h,训练图像为H,则:
1)特征框放大1倍(无放大):有(H-h+1)个特征
2)特征框放大2倍(只放大h一边,下同):有(H-2h+1)个特征
3)特征框放大3倍:有(H-3h+1)个特征
如此直到放大H/h倍
4)特征框放大H/h倍:有1个特征,即有(H-H/h*h+1)个特征
以上全部相加有:
H-h+1+H-2h+1+H-3h+1+......+H-H/h*h+1=H*H/h+H/h-h*H/h*(1+H/h)/2
设H/h=Y,则上式可变为Y(H+1-h(1+Y)/2),同理,对宽度边做同样处理可得到X(W+1-w(1+X)/2),因为这种选取符合独立同分布事件,因此总个数可以直接相乘得到,至此得到文章中的公式。
看完他的表达有一种豁然开朗的感觉!很显然,在确定了特征的形式之后,矩形特征的数量只与子窗口的大小有关。在24×24的检测窗口中,可以产生数以10万计的特征,对这些特征求值的计算量是非常大的。
由于数量的巨大,所以解决特征的快速计算将显得尤为重要。Paul Viola和Michal Jones提出使用积分图来实现特征的快速运算。构造的积分图中的像素点存储其左上方所有像素值之和,即:
![]()
其中,I(x,y)表示图像(x,y)位置的像素值。显然,积分图可以通过增量的方式通过迭代运算来实现:
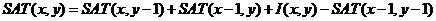
边界的初始化为:
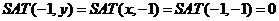
式子看上去没有想象的那么直观易懂,你可以试着在纸上画小方格,假设x=2,y=2,用上述式子来推出SAT(x,y),与你在纸上得到的SAT(x,y)比较,就会恍然大悟。
得到积分图后,计算矩形区域像素的和将只需四次查找和加减运算即可完成,如下图3所示:
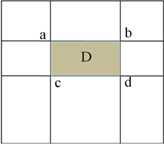
图2.积分图中矩形区域像素值和的计算示意图
假设区域D的四个顶点为a,b,c,d,则区域D内的像素和为:
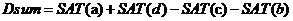
由此可以看出,积分图可以加速特征值的计算。
在了解Adaboost之前,先了解一下Boosting算法。
回答一个是与否的问题,随机猜测可以获得50%的正确率。若一种方法能获得比随机猜测稍微高一点的正确率,则称得到这个方法的过程为弱学习;若一种方法能显著提高猜测的正确率,则称得到这个方法的过程为强学习。“弱”和“强”很形象的表达了这两个过程。
1994年,Kearns和Valiant证明:在Valiant的PAC(Probably Approximately Correct)模型中,只要数据足够多,就可以将弱学习算法通过集成的方式提高至任意精度。实际上,1990年,Schapire就首先构造出一种多项式级的算法,将弱学习算法提升为强学习算法,就是最初的Boosting算法。Boosting意思为提升、加强,现在一般指将弱学习提升为强学习的一类算法。1993年,Drucker和Schapire首次以神经网络作为弱学习器,利用Boosting算法解决实际问题。前面指出,将弱学习算法通过集成的方式提高至任意精度,是Kearns和Valiant在1994年才证明的。虽然Boosting方法在1990年已经提出,但它真正成熟,也是在1994年之后才开始的。
1995年,Freund和Schapire提出了Adaboost算法,是对Boosting算法的一大提升。Adaboost是Boosting家族的代表算法之一,全称为Adaptive Boosting。Adaptively,即适应性地,该算法根据弱学习的结果反馈适应地调整假设的错误率,所以Adaboost不需要预先知道假设的错误率下限。也正因为如此,它不需要任何关于弱学习器性能的先验知识,而且和Boosting算法具有同样的效率,所以提出之后得到了广泛的应用。
传统的提升算法需要解决两个问题:(1)对于同一训练数据集,怎样改变其样本分布达到重复训练的目的;(2)弱分类器的有机组合问题。
对于这两个问题,Adaboost给出了“自适应”解决方法。首先,针对同一训练集通过赋予样本权重并在每一轮中根据分类结果改变其权重以得到同一训练集不同样本分布的目的。具体做法是通过赋予每一个训练样本一个权重来标榜其重要性,具有较大权重的样本得到更大的正确分类的概率,这样在每一轮训练中所重点关注的样本将会不同,从而达到同一样本集不同分布的目的。而样本权重的更新是基于弱学习器对于当前训练集中样本的分类正确与否,具体地,提高那些被前一轮弱分类器错误分类的样本的权值,降低那些被正确分类样本的权值,这样使下一轮弱分类器的训练更多关注错分的样本,这样,分类问题被弱分类器“分而治之”。
其次,弱分类器的组合采取加权多数表决的方法。具体地,分类误差率小的弱分类器将加大组合权重,使其在表决中有较大的“影响力”,而误差率大的弱分类器将减小其组合权重。这样,将这些在训练过程中关注不同样本不同特征的弱分类器按其分类误差率进行加权组合即构成一个分类性能更为强大的最终分类器(强分类器)。可以看到,使用Adaboost算法可以提取对分类较有影响力的特征,并将重点放在关键的训练数据上面。
Adaboost算法描述如下:
假设输入:数据集D={(x1,y1),(x2,y2),...,(xm,ym)};其中yi=0,1表示负样本和正样本;学习的循环次数为T。
过程:
1、初始化样本权重:对于yi=0,1的样本分别初始化其权重为ω1,i=1/m,1/l;其中m和l分别表示为负样本的数量和正样本的数量。
2、for t=1,...T:
①权重归一化,
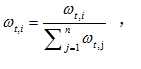
②对每个特征j,训练一个弱分类器hj(如何训练弱分类器,之后会提及),计算所有特征的加权错误率εf
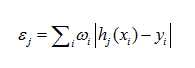
③从②确定的弱分类器中,找出一个具有最小εt的弱分类器ht;
④更新每个样本对应的权重
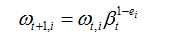
这里,如果样本xi被正确分类,则ei=0,否则ei=1,而
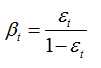
3、最终形成的强分类器组成为:
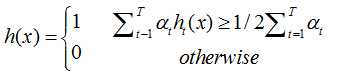
其中:
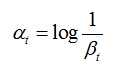
在使用Adaboost算法训练分类器之前,需要准备好正、负样本,根据样本特点选择和构造特征集。由算法的训练过程可知,当弱分类器对样本分类正确,样本的权重会减小;而分类错误时,样本的权重会增加。这样,后面的分类器会加强对错分样本的训练。最后,组合所有的弱分类器形成强分类器,通过比较这些弱分类器投票的加权和与平均投票结果来检测图像。
弱分类器之所以称为弱分类器,是因为我们并不期望选择出来的分类器具有很强的分类效果。举例说明,对于一个给定的问题,在某一轮的训练过程中,得到的弱分类器对于训练样本的分类率可能只有 51%。也就是说,只要弱分类器的分类率比随机预测略好就可以(随机预测的分类率是 50%)。在每一轮的训练结束以后,根据本轮选择出来的弱分类器对训练样本的分类正确与否,修改各个样本的权重,使得分类错误的样本权重增加。所有的训练过程结束后,产生的强分类器由各轮产生的弱分类器通过加权的投票形成。
怎么样来保证对于分类效果好的分类器赋予一个较高的权值,而对于分类效果不好的分类器赋予一个较低的权值呢?Adaboost 提供了一个很强有力的机制,把弱分类器和特征挂起勾来,把性能很好的分类器选择出来,并赋予相应的权值。将弱分类器和特征挂钩起来的一个很直接的方法是,将弱分类器和特征做一一对应的关系,也就是说,一个弱分类器仅仅依赖一个特征。为了实现这个机制,每一轮分类器的训练的过程就是选择一个矩形特征,使得这个特征能最好的将正训练样本和反训练样本分离开。弱学习过程在每一轮训练过程中,对于每一个特征来说(有很多个特征,如24*24的图片,特征的数量高达160000),都要确定一个最优阈值,使得该阈值对样本的分类效果最好。这样,每一轮训练过程都可以得到一个分类效果最好的特征(即从160000个特征中选择一个错误率最低的),而该特征所对应的弱分类器就是该轮所选出的弱分类器。
在确定了训练子窗口中的矩形特征数量和特征值后,需要对每一个特征f,训练一个弱分类器h(x,f,p,θ);

一个弱分类器是一个特征 f(x)和一个阈值θ 的混合物。训练一个弱分类器,就是在当前权重分布的情况下,确定 f(x)的最优阈值,使得这个弱分类器对所有训练样本的分类误差最低。选取一个最佳弱分类器就是选择那个对所有训练样本的分类误差在所有弱分类器中最低的那个弱分类器(特征)。

于是,通过把这个排序的表从头到尾扫描一遍就可以为弱分类器选择使分类误差 最小的阈值(最优阈值),如下图所示
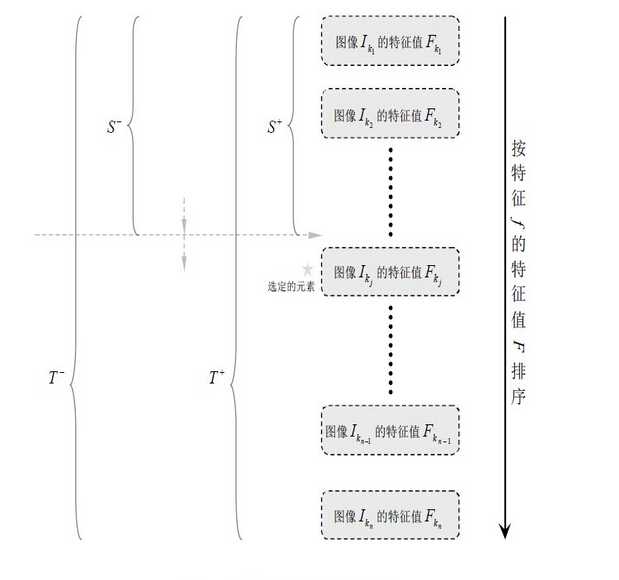
图3.训练一个弱分类器的算法
特别说明:在前期准备训练样本的时候,需要将样本归一化和灰度化到规定尺寸大小,这样每个样本的都是灰度图像并且样本的大小一致,保证了每一个Haar特征(描述的是特征的位置)都在每一个样本中出现。
在实际应用中使用一个强分类器往往无法精确解决一些复杂的分类问题,并同时达到高检出率和低误检率的要求,通常使用级联的强分类器(cascade classifier)来解决这一问题。级联分类器的策略是,将若干个强分类器由简单到复杂排列,使每级强分类器具有较高的检出率,而误检率的要求可以放低,假设每级的检出率为99.9%,误检率为50%,那么一个15级的级联分类器的检测率为0.99915≈0.9851;0.515≈0.00003,这样就可以满足现实要求了。
训练过程中,级联强分类器中的每一级分类器采用AdaBoost算法训练得到,对于第一级强分类器,训练数据为全体训练样本,指定了较高的检测率而对误检率只要求不小于随机结果,所以训练过程中一般只需用到少量分类性能较强的特征就可以达到指定要求;而对于第二级强分类器,训练数据的负样本更新为第一级强分类器对原始负样本的误检样本,这样,第下一级强分类器的训练将针对第上一级难以分开的样本进行,一般地,会使用产生稍多的特征及弱分类器,如此继续,便得到最后的由简单到复杂排列的级联强分类器。
特别说明:级联分类器中的每一强分类器都包含若干个弱分类器,而每个弱分类器都是使用前述的Adaboost算法结合Haar-like特征训练得到的。
训练过程中,级联强分类器中的每一级分类器采用AdaBoost算法训练得到,对于第一级强分类器,训练数据为全体训练样本,指定了较高的检测率而对误检率只要求不小于随机结果,所以训练过程中一般只需用到少量分类性能较强的特征就可以达到指定要求;而对于第二级强分类器,训练数据的负样本更新为第一级强分类器对原始负样本的误检样本,这样,第下一级强分类器的训练将针对第上一级难以分开的样本进行,一般地,会使用产生稍多的特征及弱分类器,如此继续,便得到最后的由简单到复杂排列的级联强分类器。
在对输入图像进行检测时,一般需要对图像进行多区域、多尺度的检测。所谓多区域,就是要对取样子窗口进行平移操作,以检测到每个区域。由于训练时候所使用的正样本都是归一化到固定尺寸的图像,所以必须使用多尺度检测以解决比训练样本尺寸更大的目标的检测。多尺度检测一般有两种策略,一种是使子窗口的尺寸固定,通过不断缩放图片来实现,显然,这种方法需要完成图像的缩放和特征值的重新计算,效率不高;而另一种方法,通过不断扩大初始化为训练样本尺寸的窗口,达到多尺度取样检测的目的,这样就避免了第一种方法的弱势。但在窗口扩大检测的过程中会出现同一个目标被多次检测的情况,所以需要进行区域的合并处理。
无论哪一种搜索方法,都会从待检测图像取样大量的子窗口图像,这些子窗口图像会被级联分类器一级一级不断地筛选,只有检出为非负区域才能进入下一步检测,否则作为非目标区域丢弃,只有通过所有级联的强分类器并判断为正区域才是最后检测得到的目标区域。级联分类器的检测过程如下图:
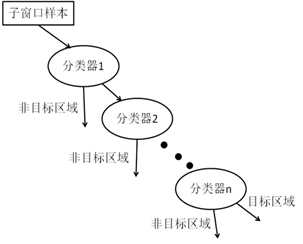
经过 Adaboost 算法的训练得到的强分类器具有最小化的错误率,而不是很高的检测率。通常,高检测率的代价是高误识率,从而引起错误率增加。要提高第i层强分类器的检测率达到di ,一个简单而有效的方法是降低强分类器的阈值;要降低第i层强分类器的误识率到fi ,一个简单而有效的方法是提高强分类器的阈值,与提高第i层强分类器的检测率相悖。通过实验结果分析,增加弱分类器个数,在提高强分类器检测率的同时降低了误识率,但该方案增加了弱分类器的个数会引起计算时间的增加。所以,构造层叠分类器时要考虑两个平衡:
构造层叠分类器的每层强分类器时就是要找到上述两个平衡的平衡点。
标签:
原文地址:http://www.cnblogs.com/codingmengmeng/p/5500566.html