标签:
1 #include<stdio.h> 2 #define MAXNODE 30 3 #define MAXCOST 32767 4 5 void Prim(int gm[][6],int closevertex[],int n)//从存储序号为0的顶点出发建立连通网的最小生成树,gm是邻接矩阵,n为顶点个数,最终建立最小生成树存于数组closevertex中 6 { 7 int lowcost[MAXNODE]; 8 int i,j,k,mincost; 9 for(i=1;i<n;i++)//初始化 10 { 11 lowcost[i]=gm[0][i];//边(u0,ui)的权值送lowcost[i] 12 closevertex[i]=0;//假定顶点ui到顶点u0有一条边 13 } 14 lowcost[0]=0;//从序号为0的顶点u0出发生成最小生成树,此时u0已经进入U集 15 closevertex[0]=0; 16 for(i=1;i<n;i++)//在n个顶点中生成有n-1条边的最小生成树(共n-1趟) 17 { 18 mincost=MAXCOST;//MOXCOST为一个极大的常量值 19 j=1;k=0; 20 while(j<n)//寻找未找到过的最小权值边 21 { 22 if(lowcost[j]!=0&&lowcost[j]<mincost) 23 { 24 mincost=lowcost[j];//记下最小权值边的权值 25 k=j;//记下最小权值边在V-U集中的顶点序号 26 27 } 28 j++;//继续寻找 29 } 30 printf("Edge:(%d,%d),Wight:%d\n",k,closevertex[k],mincost);//输出最小生成树的边与权值 31 lowcost[k]=0;//顶点k进入U集 32 for(j=1;j<n;j++) 33 if(lowcost[j]!=0&&gm[k][j]<lowcost[j])//若顶点k进入U集后使顶点k与另一顶点j(在V-U集中)构成的边权值 34 { //变小则改变lowcost[j]为这个小值,并将此最小权值的边(j,k)记入closevertex数组 35 lowcost[j]=gm[k][j]; 36 closevertex[j]=k; 37 } 38 } 39 } 40 41 void main() 42 { 43 int closevertex[MAXNODE];//存放最小生成树所有边的数组 44 int g[6][6]={{100,6,1,5,100,100},{6,100,5,100,3,100},{1,5,100,5,6,4}, 45 {5,100,5,100,100,2},{100,3,6,100,100,6},{100,100,4,2,6,100}}; 46 Prim(g,closevertex,6);//生成最小生成树 47 }
输出:
连接图和对应邻接矩阵如下:
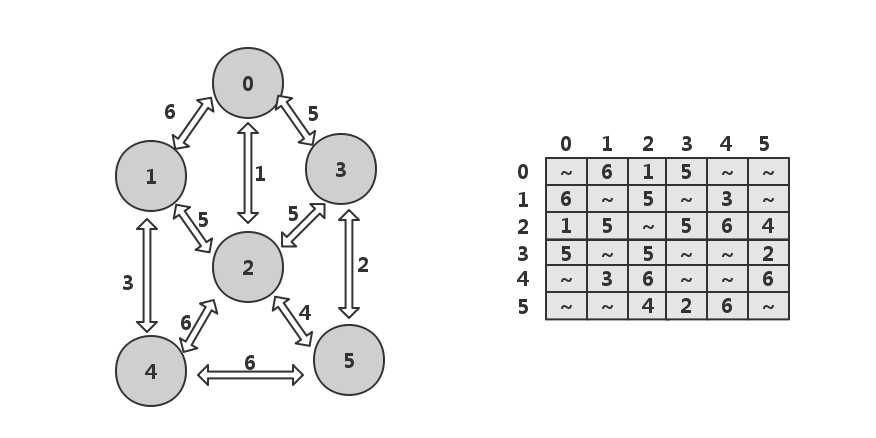
执行Prim算法产生最小生成树的分析过程见表,“---"标记的权值为每一趟所找到的最小权值。图中最小生成树每一步生长示意a~f分别对应表中的(1)~(6)趟:(1)为初始状态,(2)到(6)为生成n-1条边的n-1趟生长过程。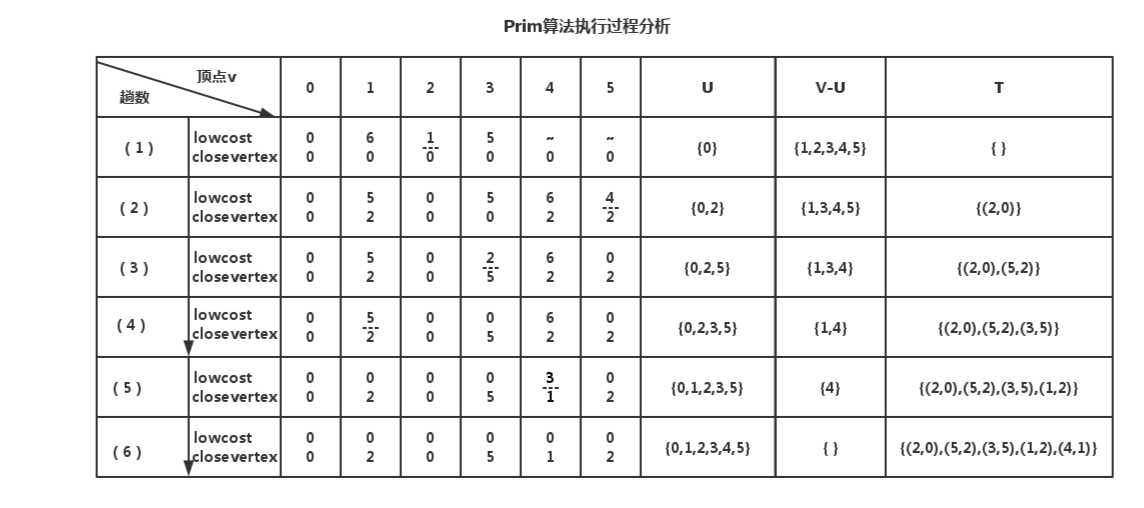
最小生成树的每一步生长情况如下图所示。其中带阴影的顶点属于U集,不带阴影的顶点属于V-U集;虚线边为待查的满足一顶点属于U集而另一顶点属于V-U集的边,而实线边则为已找到的最小生成树中的边。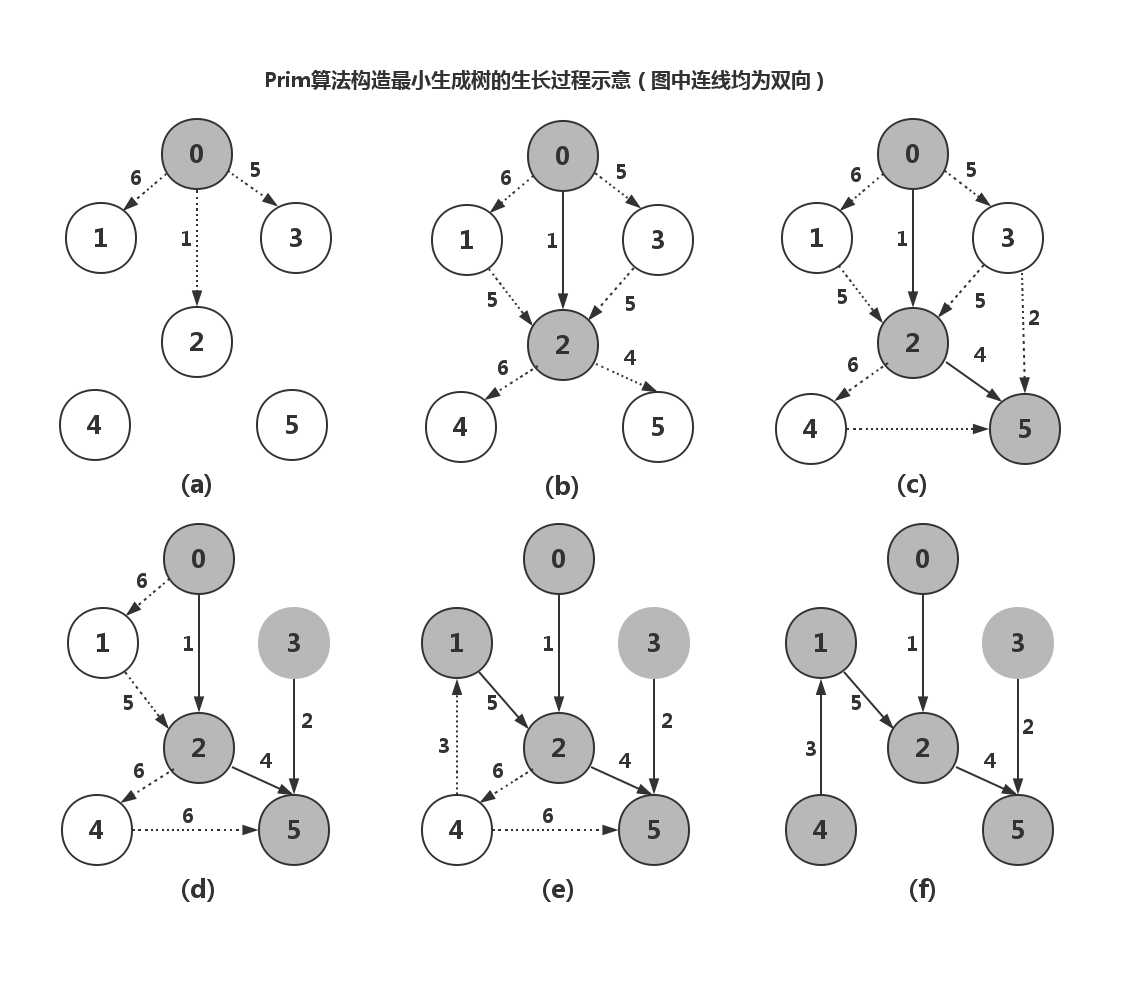
标签:
原文地址:http://www.cnblogs.com/wxdjss/p/5501127.html