This post describes how dictionaries are implemented in the Python language.
Dictionaries are indexed by keys and they can be seen as associative arrays. Let’s add 3 key/value pairs to a dictionary:
1 |
>>> d = {‘a‘: 1, ‘b‘: 2} |
4 |
{‘a‘: 1, ‘b‘: 2, ‘c‘: 3} |
The values can be accessed this way:
08 |
Traceback (most recent call last): |
09 |
File "<stdin>", line 1, in <module> |
The key ‘d’ does not exist so a KeyError exception is raised.
Hash tables
Python dictionaries are implemented using hash tables. It is an array whose indexes are obtained using a hash function on the keys. The goal of a hash function is to distribute the keys evenly in the array. A good hash function minimizes the number of collisions e.g. different keys having the same hash. Python does not have this kind of hash function. Its most important hash functions (for strings and ints) are very regular in common cases:
1 |
>>> map(hash, (0, 1, 2, 3)) |
3 |
>>> map(hash, ("namea", "nameb", "namec", "named")) |
4 |
[-1658398457, -1658398460, -1658398459, -1658398462] |
We are going to assume that we are using strings as keys for the rest of this post. The hash function for strings in Python is defined as:
01 |
arguments: string object |
06 |
set len to string‘s length |
07 |
initialize var p pointing to 1st char of string object |
08 |
set x to value pointed by p left shifted by 7 bits |
10 |
set var x to (1000003 * x) xor value pointed by p |
12 |
set x to x xor length of string object |
13 |
cache x as the hash so we don‘t need to calculate it again |
If you run hash(‘a’) in Python, it will execute string_hash() and return 12416037344. Here we assume we are using a 64-bit machine.
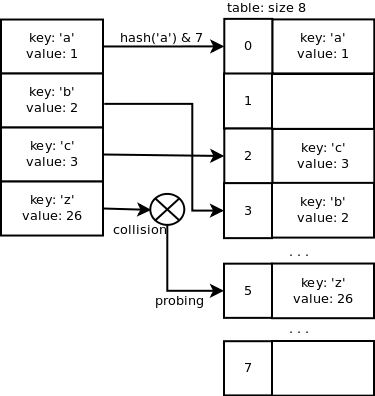
If an array of size x is used to store the key/value pairs then we use a mask equal to x-1 to calculate the slot index of the pair in the array. This makes the computation of the slot index fast. The probability to find an empty slot is high due to the resizing mechanism described below. This means that having a simple computation makes sense in most of the cases. If the size of the array is 8, the index for ‘a’ will be: hash(‘a’) & 7 = 0. The index for ‘b’ is 3, the index for ‘c’ is 2, the index for ‘z’ is 3 which is the same as ‘b’, here we have a collision.

We can see that the Python hash function does a good job when the keys are consecutive which is good because it is quite common to have this type of data to work with. However, once we add the key ‘z’, there is a collision because it is not consecutive enough.
We could use a linked list to store the pairs having the same hash but it would increase the lookup time e.g. not O(1) average anymore. The next section describes the collision resolution method used in the case of Python dictionaries.
Open addressing
Open addressing is a method of collision resolution where probing is used. In case of ‘z’, the slot index 3 is already used in the array so we need to probe for a different index to find one which is not already used. Adding a key/value pair will average O(1) and the lookup operation too.
A quadratic probing sequence is used to find a free slot. The code is the following:
1 |
j = (5*j) + 1 + perturb; |
2 |
perturb >>= PERTURB_SHIFT; |
3 |
use j % 2**i as the next table index; |
Recurring on 5*j+1 quickly magnifies small differences in the bits that didn’t affect the initial index. The variable “perturb” gets the other bits of the hash code into play.
Just out of curiosity, let’s look at the probing sequence when the table size is 32 and j = 3.
3 -> 11 -> 19 -> 29 -> 5 -> 6 -> 16 -> 31 -> 28 -> 13 -> 2…
You can read more about this probing sequence by looking at the source code of dictobject.c. A detailed explanation of the probing mechanism can be found at the top of the file.
Now, let’s look at the Python internal code along with an example.
Dictionary C structures
The following C structure is used to store a dictionary entry: key/value pair. The hash, key and value are stored. PyObject is the base class of the Python objects.
The following structure represents a dictionary. ma_fill is the number of used slots + dummy slots. A slot is marked dummy when a key pair is removed. ma_used is the number of used slots (active). ma_mask is equal to the array’s size minus 1 and is used to calculate the slot index. ma_table is the array and ma_smalltable is the initial array of size 8.
01 |
typedef struct _dictobject PyDictObject; |
07 |
PyDictEntry *ma_table; |
08 |
PyDictEntry *(*ma_lookup)(PyDictObject *mp, PyObject *key, long hash); |
09 |
PyDictEntry ma_smalltable[PyDict_MINSIZE]; |
Dictionary initialization
When you first create a dictionary, the function PyDict_New() is called. I removed some of the lines and converted the C code to pseudocode to concentrate on the key concepts.
1 |
returns new dictionary object |
3 |
allocate new dictionary object |
4 |
clear dictionary‘s table |
5 |
set dictionary‘s number of used slots + dummy slots (ma_fill) to 0 |
6 |
set dictionary‘s number of active slots (ma_used) to 0 |
7 |
set dictionary‘s mask (ma_value) to dictionary size - 1 = 7 |
8 |
set dictionary‘s lookup function to lookdict_string |
9 |
return allocated dictionary object |
Adding items
When a new key/value pair is added, PyDict_SetItem() is called. This function takes a pointer to the dictionary object and the key/value pair. It checks if the key is a string and calculates the hash or reuses the one cached if it exists. insertdict() is called to add the new key/value pair and the dictionary is resized if the number of used slots + dummy slots is greater than 2/3 of the array’s size.
Why 2/3? It is to make sure the probing sequence can find a free slot fast enough. We will look at the resizing function later.
01 |
arguments: dictionary, key, value |
02 |
returns: 0 if OK or -1 |
03 |
function PyDict_SetItem: |
08 |
call insertdict with dictionary object, key, hash and value |
09 |
if key/value pair added successfully and capacity over 2/3: |
10 |
call dictresize to resize dictionary‘s table |
inserdict() uses the lookup function lookdict_string() to find a free slot. This is the same function used to find a key. lookdict_string() calculates the slot index using the hash and the mask values. If it cannot find the key in the slot index = hash & mask, it starts probing using the loop described above, until it finds a free slot. At the first probing try, if the key is null, it returns the dummy slot if found during the first lookup. This gives priority to re-use the previously deleted slots.
We want to add the following key/value pairs: {‘a’: 1, ‘b’: 2′, ‘z’: 26, ‘y’: 25, ‘c’: 5, ‘x’: 24}. This is what happens:
A dictionary structure is allocated with internal table size of 8.
- PyDict_SetItem: key = ‘a’, value = 1
- hash = hash(‘a’) = 12416037344
- insertdict
- lookdict_string
- slot index = hash & mask = 12416037344 & 7 = 0
- slot 0 is not used so return it
- init entry at index 0 with key, value and hash
- ma_used = 1, ma_fill = 1
- PyDict_SetItem: key = ‘b’, value = 2
- hash = hash(‘b’) = 12544037731
- insertdict
- lookdict_string
- slot index = hash & mask = 12544037731 & 7 = 3
- slot 3 is not used so return it
- init entry at index 3 with key, value and hash
- ma_used = 2, ma_fill = 2
- PyDict_SetItem: key = ‘z’, value = 26
- hash = hash(‘z’) = 15616046971
- insertdict
- lookdict_string
- slot index = hash & mask = 15616046971 & 7 = 3
- slot 3 is used so probe for a different slot: 5 is free
- init entry at index 5 with key, value and hash
- ma_used = 3, ma_fill = 3
- PyDict_SetItem: key = ‘y’, value = 25
- hash = hash(‘y’) = 15488046584
- insertdict
- lookdict_string
- slot index = hash & mask = 15488046584 & 7 = 0
- slot 0 is used so probe for a different slot: 1 is free
- init entry at index 1 with key, value and hash
- ma_used = 4, ma_fill = 4
- PyDict_SetItem: key = ‘c’, value = 3
- hash = hash(‘c’) = 12672038114
- insertdict
- lookdict_string
- slot index = hash & mask = 12672038114 & 7 = 2
- slot 2 is free so return it
- init entry at index 2 with key, value and hash
- ma_used = 5, ma_fill = 5
- PyDict_SetItem: key = ‘x’, value = 24
- hash = hash(‘x’) = 15360046201
- insertdict
- lookdict_string
- slot index = hash & mask = 15360046201 & 7 = 1
- slot 1 is used so probe for a different slot: 7 is free
- init entry at index 7 with key, value and hash
- ma_used = 6, ma_fill = 6
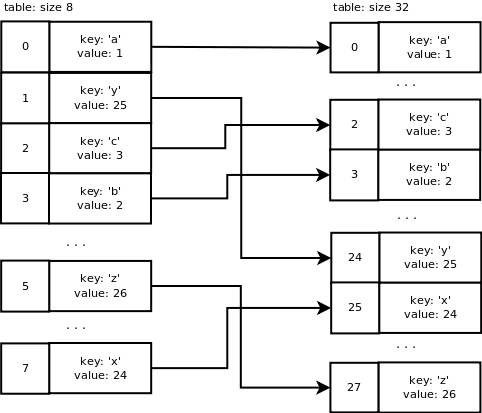
This is what we have so far:

6 slots on 8 are used now so we are over 2/3 of the array’s capacity. dictresize() is called to allocate a larger array. This function also takes care of copying the old table entries to the new table.
dictresize() is called with minused = 24 in our case which is 4 * ma_used. 2 * ma_used is used when the number of used slots is very large (greater than 50000). Why 4 times the number of used slots? It reduces the number of resize steps and it increases sparseness.
The new table size needs to be greater than 24 and it is calculated by shifting the current size 1 bit left until it is greater than 24. It ends up being 32 e.g. 8 -> 16 -> 32.
This is what happens with our table during resizing: a new table of size 32 is allocated. Old table entries are inserted into the new table using the new mask value which is 31. We end up with the following:
Removing items
PyDict_DelItem() is called to remove an entry. The hash for this key is calculated and the lookup function is called to return the entry. The slot is now a dummy slot.
We want to remove the key ‘c’ from our dictionary. We end up with the following array:






