This article describes how string objects are managed by Python internally and how string search is done.
PyStringObject structure
New string object
Sharing string objects
String search
PyStringObject structure
A string object in Python is represented internally by the structure PyStringObject. “ob_shash” is the hash of the string if calculated. “ob_sval” contains the string of size “ob_size”. The string is null terminated. The initial size of “ob_sval” is 1 byte and ob_sval[0] = 0. If you are wondering where “ob_size is defined”, take a look at PyObject_VAR_HEAD in object.h. “ob_sstate” indicates if the string object is in the interned dictionary which we are going to see later.
New string object
What happens when you assign a new string to a variable like this one?
The internal C function “PyString_FromString” is called and the pseudo code looks like this:
1 |
arguments: string object: ‘abc‘ |
2 |
returns: Python string object with ob_sval = ‘abc‘ |
3 |
PyString_FromString(string): |
4 |
size = length of string |
5 |
allocate string object + size for ‘abc‘. ob_sval will be of size: size + 1 |
Each time a new string is used, a new string object is allocated.
Sharing string objects
There is a neat feature where small strings are shared between variables. This reduces the amount of memory used. Small strings are strings of size 0 or 1 byte. The global variable “interned” is a dictionary referencing those small strings. The array “characters” is also used to reference the strings of length 1 byte: i.e. single characters. We will see later how the array “characters” is used.
1 |
static PyStringObject *characters[UCHAR_MAX + 1]; |
2 |
static PyObject *interned; |
Let’s see what happens when a new small string is assigned to a variable in your Python script.
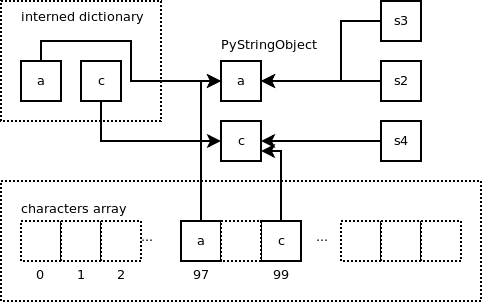
The string object containing ‘a’ is added to the dictionary “interned”. The key is a pointer to the string object and the value is the same pointer. This new string object is also referenced in the array characters at the offset 97 because value of ‘a’ is 97 in ASCII. The variable “s2” is pointing to this string object.

What happens when a different variable is assigned to the same string ‘a’?
The same string object previously created is returned so both variables are pointing to the same string object. The “characters” array is used during that process to check if the string already exists and returns the pointer to the string object.
1 |
if (size == 1 && (op = characters[*str & UCHAR_MAX]) != NULL) |

Let’s create a new small string containing the character ‘c’.
We end up with the following:
We also find the “characters” array at use when a string’s item is requested like in the following Python script:
Instead of creating a new string containing ‘a’, the pointer at the offset 97 of the “characters” array is returned. Here is the code of the function “string_item” which is called when we request a character from a string. The argument “a” is the string object containing ‘abc’ and the argument “i” is the index requested: 0 in our case. A pointer to a string object is returned.
02 |
string_item(PyStringObject *a, register Py_ssize_t i) |
07 |
pchar = a->ob_sval[i]; |
08 |
v = (PyObject *)characters[pchar & UCHAR_MAX]; |
The “characters” array is also used for function names of length 1:
String search
Let’s take a look at what happens when you perform a string search like in the following Python code:
1 |
>>> s = ‘adcabcdbdabcabd‘ |
The “find” function returns the index where the string ‘abcd’ is found in the string “s”. It returns -1 if the string is not found.
So, what happens internally? The function “fastsearch” is called. It is a mix between Boyer-Moore and Horspool algorithms plus couple of neat tricks.
Let’s call “s” the string to search in and “p” the string to search for. s = ‘adcabcdbdabcabd’ and p = ‘abcab’. “n” is the length of “s” and “m” is the length of “p”. n = 18 and m = 5.
The first check in the code is obvious, if m > n then we know that we won’t be able to find the index so the function returns -1 right away as we can see in the following code:
When m = 1, the code goes through “s” one character at a time and returns the index when there is a match. mode = FAST_SEARCH in our case as we are looking for the index where the string is found first and not the number of times the string if found.
03 |
if (mode == FAST_COUNT) { |
06 |
for (i = 0; i < n; i++) |
For other cases i.e. m > 1. The first step is to create a compressed boyer-moore delta 1 table. Two variables will be assigned during that step: “mask” and “skip”.
“mask” is a 32-bit bitmask, using the 5 least significant bits of the character as the key. It is generated using the string to search “p”. It is a bloom filter which is used to test if a character is present in this string. It is really fast but there are false positives. You can read more about bloom filters here. This is how the bitmask is generated in our case:
3 |
for (mask = i = 0; i < mlast; i++) { |
4 |
mask |= (1 << (p[i] & 0x1F)); |
7 |
mask |= (1 << (p[mlast] & 0x1F)); |
First character of “p” is ‘a’. Value of ‘a’ is 97 = 1100001 in binary format. Using the 5 least significants bits, we get 00001 so “mask” is first set to: 1 << 1 = 10. Once the entire string "p" is processed, mask = 1110. How do we use this bitmask? By using the following test where "c" is the character to look for in the string "p".
1 |
if ((mask & (1 << (c & 0x1F)))) |
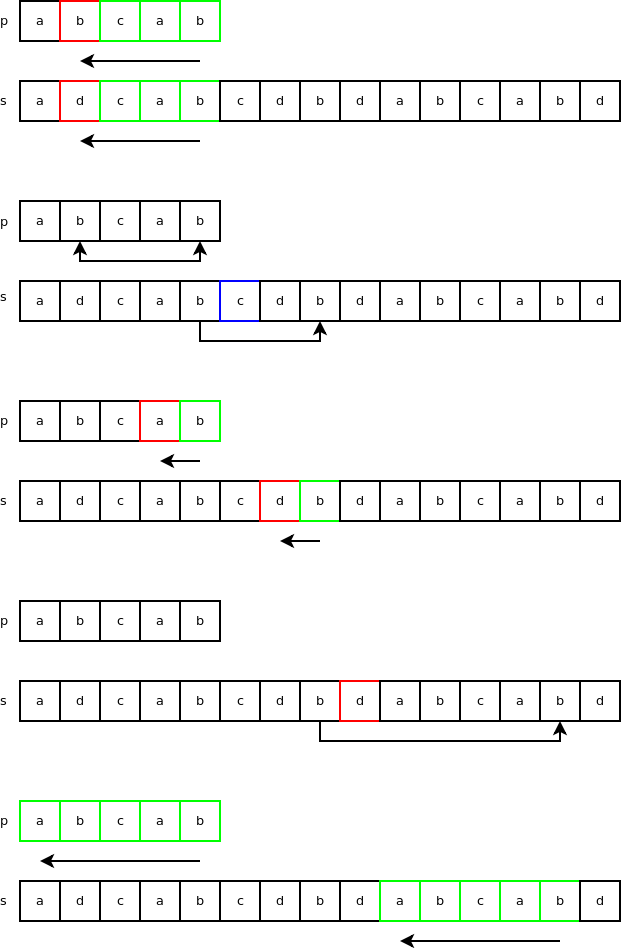
Is ‘a’ in “p” where p = ‘abcab’? Is 1110 & (1 << (‘a‘ & 0X1F)) true? 1110 & (1 << (‘a‘ & 0X1F)) = 1110 & 10 = 10. So, yes ‘a‘ is in ‘abcab‘. If we test with ‘d‘, we get false and also with the characters from ‘e‘ to ‘z‘ so this filter works pretty well in our case. "skip" is set to the index of the character with the same value as the last character in the string to search for. "skip" is set to the length of "p" - 1 if the last character is not found. The last character in the string to search for is ‘b‘ which means "skip" will be set to 2 because this character can also be found by skipping over 2 characters down. This variable is used in a skip method called the bad-character skip method. In the following example: p = ‘abcab‘ and s = ‘adcabcaba‘. The search starts at index 4 of "s" and checks backward if there is a string match. This first test fails at index = 1 where ‘b‘ is different than ‘d‘. We know that the character ‘b‘ in "p" is also found 3 characters down starting from the end. Because ‘c‘ is part of "p", we skip to the following ‘b‘. This is the bad-character skip. 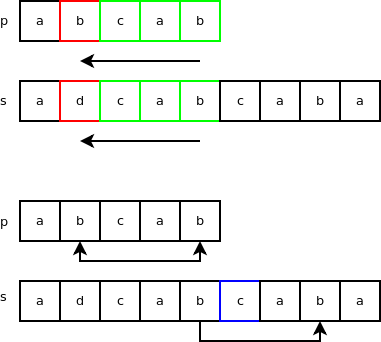
Next is the search loop itself (real code is in C instead of Python):
01 |
for i = 0 to n - m = 13: |
02 |
if s[i+m-1] == p[m-1]: |
03 |
if s[i:i+mlast] == p[0:mlast]: |
The test “s[i+m] not in p” is done using the bitmask. “i += skip” is the bad-character skip. “i += m” is done when the next character is not found in “p”.
Let’s see how this search algorithm works with our strings “p” and “s”. The first 3 steps are familiar. After that, the character ‘d’ is not in the string “p” so we skip the length of “p” and quickly find a match after that.