标签:
leetcode上的28. Implement strStr()就是一个字符串匹配问题。字符串匹配是计算机的基本任务之一。所以接下来的两篇日志,都对相关的算法进行总结。
如果用暴力匹配的思路,并假设现在文本串S匹配到 i 位置,模式串P匹配到 j 位置,则有:
1 class Solution { 2 public: 3 int strStr(string haystack, string needle) { 4 if(needle=="") return 0; 5 int i = 0,j = 0; 6 while(i<haystack.size()){ 7 int tagi; 8 tagi = i; 9 while((haystack[tagi] == needle[j])&&j<needle.size()){ 10 tagi++; 11 } 12 if(j==needle.size()){ 13 14 return tagi-needle.size(); 15 }else{ 16 j = 0; 17 } 18 i++; 19 } 20 return -1; 21 } 22 }
该部分内容转载自阮一峰
1.

首先,字符串"BBC ABCDAB ABCDABCDABDE"的第一个字符与搜索词"ABCDABD"的第一个字符,进行比较。因为B与A不匹配,所以搜索词后移一位。
2.

因为B与A不匹配,搜索词再往后移。
3.

就这样,直到字符串有一个字符,与搜索词的第一个字符相同为止。
4.

接着比较字符串和搜索词的下一个字符,还是相同。
5.

直到字符串有一个字符,与搜索词对应的字符不相同为止。
6.

这时,最自然的反应是,将搜索词整个后移一位,再从头逐个比较。这样做虽然可行,但是效率很差,因为你要把"搜索位置"移到已经比较过的位置,重比一遍。
7.

一个基本事实是,当空格与D不匹配时,你其实知道前面六个字符是"ABCDAB"。KMP算法的想法是,设法利用这个已知信息,不要把"搜索位置"移回已经比较过的位置,继续把它向后移,这样就提高了效率。
8.

怎么做到这一点呢?可以针对搜索词,算出一张《部分匹配表》(Partial Match Table)。这张表是如何产生的,后面再介绍,这里只要会用就可以了。
9.

已知空格与D不匹配时,前面六个字符"ABCDAB"是匹配的。查表可知,最后一个匹配字符B对应的"部分匹配值"为2,因此按照下面的公式算出向后移动的位数:
移动位数 = 已匹配的字符数 - 对应的部分匹配值
因为 6 - 2 等于4,所以将搜索词向后移动4位。
10.

因为空格与C不匹配,搜索词还要继续往后移。这时,已匹配的字符数为2("AB"),对应的"部分匹配值"为0。所以,移动位数 = 2 - 0,结果为 2,于是将搜索词向后移2位。
11.

因为空格与A不匹配,继续后移一位。
12.

逐位比较,直到发现C与D不匹配。于是,移动位数 = 6 - 2,继续将搜索词向后移动4位。
13.

逐位比较,直到搜索词的最后一位,发现完全匹配,于是搜索完成。如果还要继续搜索(即找出全部匹配),移动位数 = 7 - 0,再将搜索词向后移动7位,这里就不再重复了。
14.

下面介绍《部分匹配表》是如何产生的。
首先,要了解两个概念:"前缀"和"后缀"。 "前缀"指除了最后一个字符以外,一个字符串的全部头部组合;"后缀"指除了第一个字符以外,一个字符串的全部尾部组合。
15.

"部分匹配值"就是"前缀"和"后缀"的最长的共有元素的长度。以"ABCDABD"为例,
- "A"的前缀和后缀都为空集,共有元素的长度为0;
- "AB"的前缀为[A],后缀为[B],共有元素的长度为0;
- "ABC"的前缀为[A, AB],后缀为[BC, C],共有元素的长度0;
- "ABCD"的前缀为[A, AB, ABC],后缀为[BCD, CD, D],共有元素的长度为0;
- "ABCDA"的前缀为[A, AB, ABC, ABCD],后缀为[BCDA, CDA, DA, A],共有元素为"A",长度为1;
- "ABCDAB"的前缀为[A, AB, ABC, ABCD, ABCDA],后缀为[BCDAB, CDAB, DAB, AB, B],共有元素为"AB",长度为2;
- "ABCDABD"的前缀为[A, AB, ABC, ABCD, ABCDA, ABCDAB],后缀为[BCDABD, CDABD, DABD, ABD, BD, D],共有元素的长度为0。
16.

"部分匹配"的实质是,有时候,字符串头部和尾部会有重复。比如,"ABCDAB"之中有两个"AB",那么它的"部分匹配值"就是2("AB"的长度)。搜索词移动的时候,第一个"AB"向后移动4位(字符串长度-部分匹配值),就可以来到第二个"AB"的位置。
1 vector<int> next(needle.size(),0); 2 int k = 0; 3 for(int i = 1;i<needle.size();i++){ 4 //阶段三,在此之前都匹配,该值不匹配 5 //寻找更小的匹配序列,递归调用,找到匹配的序列,若没有找到,到k为0停止 6 while(k>0&&(needle[k]!=needle[i])){ 7 k = next[k-1]; 8 } 9 //阶段一,还未发现任何一个重复匹配值。直接执行i++,继续寻找 10 //阶段二,找到重复匹配值,k++ 11 if(needle[k] == needle[i]){ 12 ++k; 13 } 14 next[i] = k; 15 }
在上图中,使用next[]数组来保存匹配表。匹配表初始化为长度与待查字符串相等,默认值均为0的数组。生成字符串的匹配表过程分为三个阶段:
1、还未发现任何一个重复的匹配值,直接向后遍历,执行i++,匹配表保持默认值0。
2、找到重复的匹配值,k++。
3、在该值以前的字符串都匹配,在此处的字符不匹配。我们递归调用k = next[k-1]来寻找更短的匹配字符串。
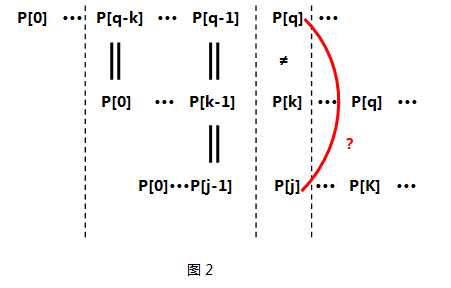
对于第三个阶段,

1 class Solution { 2 public: 3 int strStr(string haystack, string needle) { 4 5 if(needle.empty()) return 0; 6 if(haystack.empty()) return -1; 7 //pre config,create the next[] 8 vector<int> next(needle.size(),0); 9 int k = 0; 10 for(int i = 1;i<needle.size();i++){ 11 //阶段三,在此之前都匹配,该值不匹配 12 //寻找更小的匹配序列,递归调用,找到匹配的序列,若没有找到,到k为0停止 13 while(k>0&&(needle[k]!=needle[i])){ 14 k = next[k-1]; 15 } 16 //阶段一,还未发现任何一个重复匹配值。直接执行i++,继续寻找 17 //阶段二,找到重复匹配值,k++ 18 if(needle[k] == needle[i]){ 19 ++k; 20 } 21 next[i] = k; 22 } 23 int j=0;//用来判断needle到哪一位 24 //match 25 for(int i = 0;i<haystack.size();i++){ 26 //阶段1,未发现相同的值,i++,j=0 27 //阶段2,发现相同的值,i++,j++ 28 //阶段3,j==needle.size(),找到合适的项,返回i-j,估计i j都大1 29 //阶段4分支,j>0,值不同,j = next[j-1];i不变,重新比较,再不同,再计算j = next[j-1],相同转2或者j==0转1 30 //阶段5,i==hay.size()没找到,返回-1. 31 while((haystack[i]!=needle[j])&&j>0){ 32 j = next[j-1]; 33 } 34 if(needle[j] == haystack[i]){ 35 j++; 36 } 37 if(j == needle.size()){ 38 //j比实际值大1,而i加1的操作在本次for循环最后才执行。 39 return i-j+1; 40 } 41 return -1; 42 43 } 44 };
标签:
原文地址:http://www.cnblogs.com/timesdaughter/p/5520828.html