关于NSString的算法题目

时间：2016-05-27 12:48:00 阅读：229 评论：0 收藏：0 [点我收藏+]

标签：

有如下业务：

富文本中带有自定义的表情图片的转义字符（哈哈我抓到你了/大笑表情，太开心了/邪恶的表情），这段字符串中“/大笑表情”及“/邪恶的表情”分别表示一个表情图片。程序中有一个表情转义字符和表情图片名称对照的json文件。现在需要实现一个算法，可以将富文本中的转义字符通过查找json文件找出来。

思路：

1、建立树结构，将转义字符和表情图片名称对应起来，可以存储上一次查找的结果；

2、从“/”开始截取字符串，依次进行“/A”在树结构中查找，查找方法如二分法查找，查找到后记录全部吻合的查询结果（如放在数组中），如果没有查询到则返回无结果；

3、在符合查询结果的数组中继续用“/AB”进行查找，保存吻合的查询结果到数组中；

4、依次类推，最终找到符合结果的转义字符对应的图片名称；

5、字符查找中可以使用字符串搜索查找相关的算法进行（如KMP算法）。

单模式字符串匹配

1. 朴素算法

朴素算法的问题在于不够智能，有些位置明显没有必要进行比较操作，但这个算法无法区分出来，还是继续比较，浪费了资源。

2. KMP算法

在KMP算法中，引入了前缀函数的概念，从而可以更加精确的知道：当不匹配发生时，应该跳过多少个字符。下面介绍前缀函数。

字符串A = "abcde" B = "ab"。那么就称字符串B为A的前缀，记为B ? A。同理可知 C = "e","de" 等都是 A 的后缀，以为C ? A。

技术分享

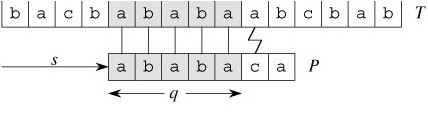
这里模式串 P = “ababaca”,在匹配了 q=5 个字符后失配，因此，下一步就是要考虑将P向右移多少位进行新的一轮匹配检测。朴素算法中，直接将P右移1位，也就是将P的首字符‘a‘去和目标串的‘b‘字符进行检测，这明显是多余的。通过我们肉眼的观察，可以很简单的知道应该将模式串P右移到下图‘a3‘处再开始新一轮的检测，直接跳过肯定不匹配的字符‘b‘，那么我们“肉眼”观察的这一结果怎么把它用语言表示出来呢？

技术分享

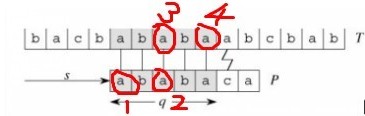
我们的观察过程是这样的：

1. P的前缀"ab"中‘a‘ != ‘b‘，又因该前缀已经匹配了T中对应的"ab"，因此，该前缀的字符‘a1‘肯定不会和T中对应的字串"ab"中的‘b‘匹配，也就是将P向右滑动一个位移是无意义的。
2. 接下来考察P的前缀"aba"，发现该前缀自身的前缀‘a1‘与自身后缀‘a2‘相等，"a1 b a2" 已经匹配了T中的"a b a3"，因此有 ‘a2‘ == ‘a3‘, 故得到 ‘a1‘ == ‘a3‘......
3. 利用此思想，可推知在已经匹配 q=5 个字符的情况下，将P向右移当且仅当 2个位移时，才能满足既没有冗余(如把‘a‘去和‘b‘比较)，又不会丢失(如把‘a1‘ 直接与 ‘a4‘ 开始比较，则丢失了与‘a3‘的比较)。
4. 而前缀函数就是这样一种函数，它决定了q与位移的一一对应关系，通过它就可以间接地求得位移s。
好后缀算法

这样的观察过程并不具有一般性，下面是《算法导论》中对前缀函数的形式化说明：

已知一个模式P[1. . m]，模式P的前缀函数是函数π{1,2,. . . , m}->{0,1, 2,. . . ,m-1}并满足

π[q]=max{k:k<q 且Pk? Pq}

即π[q]是Pq的真后缀P的最长前缀的长度（此是《算法导论》中原话，但不是很好理解，其实就是Pq中即是自己的真后缀，又是自己最长前缀的字符串的最大长度）。下面举例说明（模式P=ababababca）

i=1时，a真后缀为空；i=2时，ab真后缀为b，不是自己的前缀；i=3时，aba真后缀为a, ab，且a和ab都是aba的前缀，ab最长，故为2；。。。

KMP算法中，如果q+1时发生不匹配，则可以向前移动q-π[q]位。

#include <iostream>

using namespace std;

when searching a pattern in a string, and mismatch happened, we can skip more chars, instead of going through one by one;

the skip rule is that:

1. if position p mismatched, we need consider the chars in 0- (p-1);

2. whether [0,k-1](prefix substring) matched with [p-k,p-1](suffix substring),if matched, we can align the pattern to p-k;and do comparation from p again.

below function is get the k for different p, more information refer to comments inline;

void get_skippattern(char *pattern, int* next, int len)

{

int pos = 2;

int subStrIndex = 0; //valid prefix candidate substring index;

next[0] = -1; // when 1st char mismatched, always move 1 (p=0, k=-1);

next[1] = 0; // when 2nd mismatched, always move 1(p=1, k=0);in fact, if the 2nd char is same as 1st char, we can move 2

while(pos<len)

{

if(pattern[pos - 1] == pattern[subStrIndex]) //one char matched, then continue to match more,

{

subStrIndex++; //prefix substring move ahead;

next[pos] = subStrIndex;//for current position, the k is got;

pos++; //current pos move ahead;

}

else if(subStrIndex>0) //one substring found, but in the new pos, mismatched;

{

subStrIndex = next[subStrIndex]; //then we need fall back subStrIndex to value that still can be matched;

}

else

{

next[pos] = 0;

pos++;

}

for(int i =0;i<len;i++)

cout<<next[i]<<" ";

}

int KMP_search(char *src, int slen, char *pattern, int plen)

{

int* next = (int *)malloc(sizeof(int)*slen);

get_skippattern(pattern,next,plen);

int indexInSrc = 0;

int offset = 0;

while((indexInSrc+offset)<slen)

{

if(pattern[offset] == src[indexInSrc+offset])

{

if(offset == (plen-1))

return indexInSrc;

offset++;

}else

{

indexInSrc += offset-next[offset];

if(next[offset]>-1)

offset = next[offset];

else

offset = 0;

}

return slen;

}

int main (int argc, char ** argv)

{

//char *pat = "ABCDABDEF";

//char *src = "ABC ABCDAB ABCDABCDABDEF";

char *pat="ABABETTABABABYUABCD";

char *src = "ABCDEABCDGABCDETTABCDFABCDETTABCDATYUABCD";

int index = KMP_search(src,strlen(src),pat,strlen(pat));

cout<<"found pattern in "<<index<<endl;

return 0;

}

3. BM算法

BM算法的特殊之处在于BM是右向左匹配，同时结合坏字符和好后缀两个规则使得移动距离最大。下面分别介绍坏字符和好后缀规则：

如果程序匹配了一个好后缀, 并且在模式中还有另外一个相同的后缀, 那

把下一个后缀移动到当前后缀位置。好后缀算法有两种情况：

Case1：模式串中有子串和好后缀安全匹配，则将最靠右的那个子串移动到好后缀的位置。继续进行匹配。

Case2：如果不存在和好后缀完全匹配的子串，则在好后缀中找到具有如下特征的最长子串,使得P[m-s…m]=P[0…s]。说不清楚的看图。

技术分享

给一些具体的例子

当出现一个坏字符时, BM算法向右移动模式串, 让模式串中最靠右的对应字符与坏字符相对，然后继续匹配。坏字符算法也有两种情况。

Case1：模式串中有对应的坏字符时，见图。

Case2：模式串中不存在坏字符。见图。

技术分享

BM算法的移动规则是：

将概述中的++j，换成j+=MAX（shift（好后缀），shift（坏字符）），即BM算法是每次向右移动模式串的距离是，按照好后缀算法和坏字符算法计算得到的最大值。

shift（好后缀）和shift（坏字符）通过模式串的预处理数组的简单计算得到。好后缀算法的预处理数组是bmGs[]，坏字符算法的预处理数组是BmBc[]。

下面先解释这两个数组的意义：

BmBc 的定义：

1、字符在模式串中没有出现：，如模式串中没有字符p，则BmBc[‘p’] = strlen(模式串)。

2、字符在模式串中有出现。如下图，BmBc[‘k’]表示字符k在模式串中最后一次出现的位置，距离模式串串尾的长度。

如果只考虑坏字符，应该移动多少呢？下面的图里有3个例子：

技术分享

示例1中，在b和c比较时发生了不match，这时，我们的BmBc[‘c’] = 3，这时我们应该移动多少呢，移动-1,如何计算的呢？ BmBc[‘c’] – strlen(pat) +1 + i (index of pattern string)

实例2中，b和a发生不match，这时，BmBc[‘a’] = 6, 应该移动6-7+1+2 = 2；

实例3中，b和y发生不match，这时，BmBc[‘y’] = 7，应该移动7-7+1+1 = 2;

对于这里BmBc的定义，和shift的值的计算是很难让人理解的，我们是不是可以简单一点定义BmBc[char] 表示char在pattern中最后出现的位置，如果不出现为pattern的长度，i是不match的index，shift的距离就是BmBc[char]-i。

还有就是，在实例1中，我们真的要去移动-1吗，其实没有必要了，如果只用坏字符，你可以想想怎么做；但如果考虑上好后缀就不用额外考虑了。

为了实现好后缀规则，需要定义一个数组suffix[]，其中suffix[i] = s 表示以i为起点（包含i，从右往左匹配），与模式串后缀匹配的最大长度，如下图所示，用公式可以描述：满足P[i-s, i] == P[m-s, m]的最大长度s。

suffix[m-1]=m;

for (i=m-2；i>=0；--i)

{

q=i;

while(q>=0&&P[q]==P[m-1-i+q])

--q;

suffix[i]=i-q;

}

有了suffix[i]，如何计算BmGc？

bmGs的定义(BmGs数组的下标是数字，表示字符在模式串中位置), BmGs数组的定义，分三种情况：

1、模式串中有子串匹配上好后缀

技术分享

在这个视角图1中，在i处发生不匹配，从i开始从右向左搜索子字符串，在视图2中试图找到不匹配的字符和子串匹配位置的关系。视图2中i开始的子串与后缀匹配，那可以知道后缀的长度就是Suffix[i]，再往左移动一下就是不匹配的位置了，而这时应该移动的距离是m-1-i，也就是式子bmGs[m-1-suff[i]] = m- 1 – i;

模式串中没有子串匹配上好后缀，但找到一个最大前缀

技术分享

在这种情况下，空白位置发生不匹配时，其好后缀都是最前面的两个，那么其移动的距离其实跟不匹配的位置 j 没有关系，只与最好前缀的位置i有关，所以，bmGs[j] = m- 1 – i;

模式串中没有子串匹配上好后缀，但找不到一个最大前缀

技术分享

没有任何子串匹配的时候，那就移动模式串的长度。

举例如下：

技术分享

实现代码如下：

void preBmGs(char *x,int m,int bmGs[]) {

int i, j, suff[XSIZE];

suffixes(x, m, suff);

for (i =0; i < m; ++i)

bmGs[i] = m;

j =0;

for (i = m -1; i >= 0; --i)

if (suff[i] == i +1)

for (; j < m -1 - i; ++j)

if (bmGs[j] == m)

bmGs[j] = m -1 - i;

for (i =0; i <= m - 2; ++i)

bmGs[m -1 - suff[i]] = m -1 - i;

}

下面来完整实现一下BM算法吧：

#include<stdlib.h>

#include<stdio.h>

#include<string.h>

constint CHAR_COUNT =26;// only lower case ASCII char

void calculateBmBc(constchar *s,int len, int *BmBc)

{

int i=0;

for(i =0; i<CHAR_COUNT;i++)

{

BmBc[i] = len;

}

for(i =0;i<len;i++)

{

BmBc[s[i]-‘a‘] = i;

}

void calculateSuffix(constchar *s,int len,int *suffix)

{

int i = len -1;

int j =0;

suffix[len-1] = len;

for(;i>=0;i--)

{

j =0;

while(j<(len-1) && s[i-j] == s[len-1-j])

j++;

suffix[i] = j;

}

void calculateBmGs(constchar *s,int len,int *BmGs)

{

int* suffix = (int *)malloc(sizeof(int)*len);//new int[len];

int i =0;

int j =0;

calculateSuffix(s,len,suffix);

for(i=0;i<len;i++)// init the array, and also cover case 3

{

BmGs[i] = len;

}

for(i=len-1;i>=0;i--)

{

if(suffix[i] == i+1)// prefix of the string matched with suffix, case 2

{

for(j =0;j<len-1-i;j++)

{

if(BmGs[j] == len)

BmGs[j] = len -1 - i;

}

for(i =0;i<=len-2;i++)// case 1;

{

BmGs[len-1-suffix[i]] = len-1-i;

}

free(suffix);

}

int BMSearch(constchar *src,int srclen,constchar *pattern,int patlen)

{

int i=0;

int * BmGs = (int *)malloc(sizeof(int)*(patlen));

int * BmBc = (int *)malloc(sizeof(int)*(CHAR_COUNT));

calculateBmBc(pattern, patlen, BmBc);

calculateBmGs(pattern,patlen, BmGs);

for(i =0;i<(srclen-patlen);)

{

int j = patlen-1;

while(j>=0 && src[i+j] == pattern[j]) j--;

if(j <0)

return i;

else

i += BmGs[j]>(j-BmBc[j])?BmGs[j]:(j-BmBc[j]);

}

free(BmGs);

free(BmBc);

return srclen;

}

int main(int argc,char **argv)

{

int i =BMSearch("GCAGAGAG",8,"AGAG",4);

printf("found pattern at %d",i);

return0;

}

4、SUNDAY 算法描述：

字符串查找算法中，最著名的两个是KMP算法（Knuth-Morris-Pratt)和BM算法（Boyer-Moore)。两个算法在最坏情况下均具有线性的查找时间。但是在实用上，KMP算法并不比最简单的c库函数strstr()快多少，而BM算法则往往比KMP算法快上3－5倍。但是BM算法还不是最快的算法，这里介绍一种比BM算法更快一些的查找算法。

例如我们要在"substring searching algorithm"查找"search"，刚开始时，把子串与文本左边对齐：

substring searching algorithm

结果在第二个字符处发现不匹配，于是要把子串往后移动。但是该移动多少呢？这就是各种算法各显神通的地方了，最简单的做法是移动一个字符位置；KMP是利用已经匹配部分的信息来移动；BM算法是做反向比较，并根据已经匹配的部分来确定移动量。这里要介绍的方法是看紧跟在当前子串之后的那个字符（上图中的 ‘i‘)。

显然，不管移动多少，这个字符是肯定要参加下一步的比较的，也就是说，如果下一步匹配到了，这个字符必须在子串内。所以，可以移动子串，使子串中的最右边的这个字符与它对齐。现在子串‘search‘中并不存在‘i‘，则说明可以直接跳过一大片，从‘i‘之后的那个字符开始作下一步的比较，如下图：

substring searching algorithm

比较的结果，第一个字符就不匹配，再看子串后面的那个字符，是‘r‘,它在子串中出现在倒数第三位，于是把子串向前移动三位，使两个‘r‘对齐，如下：

substring searching algorithm

哈！这次匹配成功了！回顾整个过程，我们只移动了两次子串就找到了匹配位置，是不是很神啊?!可以证明，用这个算法，每一步的移动量都比BM算法要大，所以肯定比BM算法更快。

代码如下：

const char* sunday(const char* str, const char* subStr)

{

const int maxSize=256;