标签:
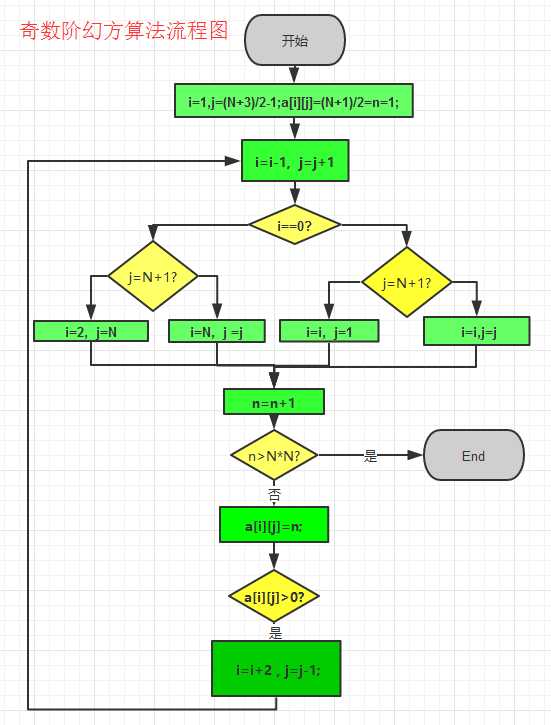
一、设计的流程图如下所示
二、Java 语言的代码实现
package MagicSquare; //奇数幻方的实现 public class Magic_Odd { //n 为幻方的阶数 public static int[][] magicOdd(int n) { //构造一个(n+2)*(n+2)阶的方阵 int[][] square = new int[n + 1][n + 1]; int i = 0; int j = (n + 1) / 2; //从第一行的中间那个数字(是1)开始填幻方 //n阶幻方一共有n*n个数字(从1~n*n) //奇数阶幻方的实现算法 for (int key = 1; key <= n * n; key++) { if ((key % n) == 1) i++; else { //填充当前数的右上角那个数 i--; j++; } if (i == 0) {//判断条件:若是在(n+2)*(n+2)阶方阵的第一行 if(j==n+1){ i=2; j=n; }else{ i=n; } } else{ if(j==n+1){ j=1; } } square[i][j] = key; } //对(n+2)*(n+2)阶的方阵进行筛选出中间的n*n阶幻方 int[][] matrix = new int[n][n]; for (int k = 0; k < matrix.length; k++) { for (int l = 0; l < matrix[0].length; l++) { matrix[k][l] = square[k + 1][l + 1]; } } return matrix; } //测试函数 public static void main(String[] args) { int[][] magic = Magic_Odd.magicOdd(11); //测试11阶幻方 for (int k = 0; k < magic.length; k++) { for (int l = 0; l < magic[0].length; l++) { System.out.print(magic[k][l] + " "); } System.out.println(); } } }
三、测试结果:
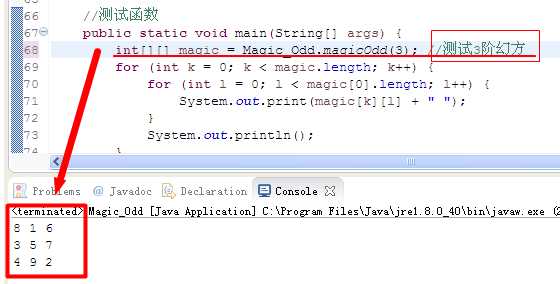
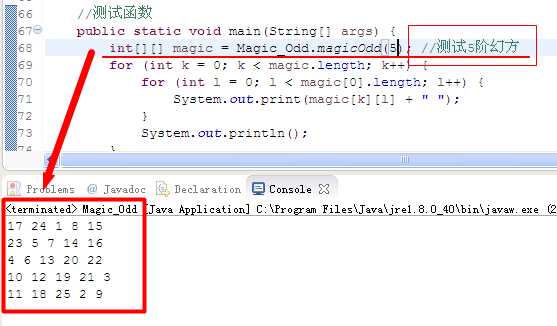
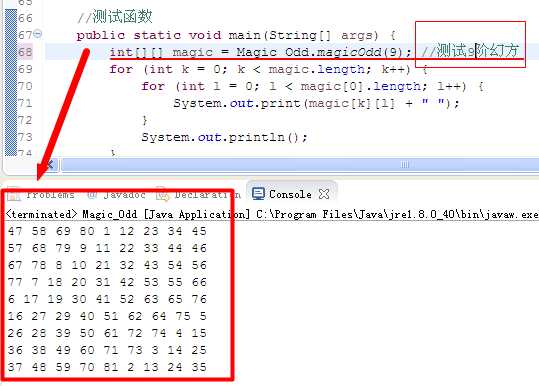
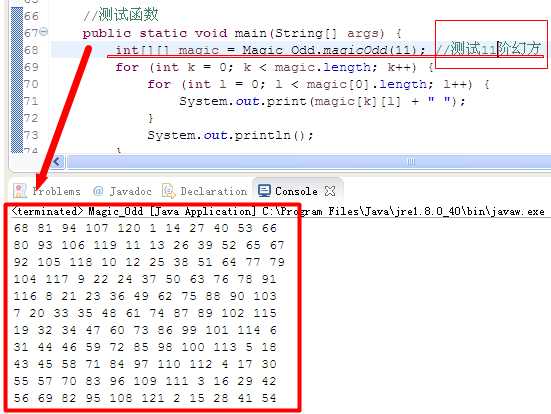
(相关源码资源详见:https://github.com/shenxiaolinZERO/Resources/tree/master/Resources/Magic_Test)
标签:
原文地址:http://www.cnblogs.com/shenxiaolin/p/5538364.html