标签:
又称二叉查找树,简称BST。具有以下性质的二叉树:
(1) 若左子树非空,则左子树上所有结点值均小于根结点的值
(2) 若右子树非空,则右子树上所有结点值均大于根结点的值
(3) 左,右子树本身也分别是一棵二叉排序树
也是一个递归的数据结构。下图是一个二叉排序树。
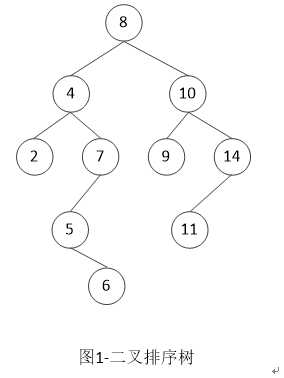
对其进行中序遍历得到一个递增的有序序列,如上图的中序序列为2,4,5,6,7,8,9,10,11,14。
二叉排序树是一种动态的集合,插入结点的过程为,结点值小于根结点值,插入到左子树中,若大于根结点值,则插入到右子树中。插入的新结点一定是某个叶结点。
/**
* 在二叉排序树node中插入一个值为info的结点
* @param node 二叉排序树
* @param info 待插入结点值
* @return
*/
public Node insert(Node node, Integer info){
if(node == null){
node = new Node();
node.data = info;
}
if(info < node.data){
node.lchild = insert(node.lchild, info);
} else if(info > node.data){
node.rchild = insert(node.rchild, info);
} else { }
return node;
}
从根结点开始,若给定值等于根结点值,则查找成功;若小于根结点值,在左子树中查找,否则在右子树中查找。可分为递归和非递归实现。
/**
* 二叉排序树,查找,递归实现
* @param root
* @param inte
* @return -1 不存在 1 存在
*/
public int searchRecur(Node root, Integer inte){
if(root!= null){
if(inte == root.data ){
return 1;
} else if(inte < root.data){
return searchRecur(root.lchild, inte);
} else if(inte > root.data){
return searchRecur(root.rchild, inte);
}
}
return -1;
}
/**
* 查找, 非递归实现
* @return -1 不能存在 1 存在
*/
public int search(Node root, Integer inte){
while(root != null && inte != root.data){
if(inte < root.data){
root = root.lchild;
} else {
root = root.rchild;
}
}
return root == null ? -1 : 1;
}
依次输入数据元素,插入到合适的位置上,具体的过程是,每读入一个元素,建立一个新结点,若新结点值小于根结点值,则插入到左子树中,否则插入到右子树中。
public class BST {
Node root;
int n=1; // 结点总数
private class Node{
Integer data;
Node lchild, rchild;
}
public BST(){
build(); // 递归构造
System.out.println("根结点:" + root.data);
btDepth();
}
/**
* 构造一棵二叉排序树
*/
public void build(){
// Integer[] ins = new Integer[] { 8, 4, 9, 2, 7, 5, 6 };
Integer[] ins = new Integer[] { 8, 4, 2, 7, 5, 6, 16, 10, 9, 14, 15, 11, 12};
root = new Node();
root.data = ins[0];
for (int i = 1; i < ins.length; i++) {
insert(root, ins[i]);
n++;
}
}
}
删除一个结点时,必须保证二叉排序树的性质不会丢失。删除操作的实现过程按3种情况来处理:
(1)若删除的结点 n 是叶子结点,则直接删除,不会破坏二叉排序树性质;
(2)若删除的结点 n 只有一棵左子树或者右子树,则使用左或右子女替换;
(3)若删除的结点 n 左右子树均不空,则令n的直接后继(或直接前驱)替代n,然后删除这个直接后继(或前驱)。
/**
* 先找到该结点及其双亲结点,然后根据规则删除
* @param root 根节点
* @param del 待删除结点值
* @return -1结点不存在 1删除成功
*/
public int delete(Node root, Integer del){
Node pre = null; // 待删除结点的双亲结点
/*
* 首先找到该结点
*/
while(root != null && del != root.data){
pre = root;
if(del < root.data){
root = root.lchild;
} else {
root = root.rchild;
}
}
if(root == null){ // 若不存在 直接返回
return -1;
}
delete(root, pre);
return 1;
}
/**
* 删除结点有三种情况
* <ul>
* <li> 若删除的结点 n 是叶子结点,则直接删除;
* <li> 若删除的结点 n 只有一棵左子树或者右子树,则使用左或右子女替换;
* <li> 若删除的结点 n 左右子树均不空,则令n的直接后继(或直接前驱)替代n,然后删除这个直接后继(或前驱)
* <p> 这里的直接前驱和后继是针对中序遍历的顺序而言
* <ul/>
* @param node 待删除结点
* @param pre 其双亲结点
*/
private void delete(Node node, Node pre) {
Node tmp = null;
if(node.lchild == null && node.rchild == null){ // 叶子结点
tmp = null;
} else if (node.lchild == null) { // 左孩子为空,直接用右孩子替代
tmp = node.rchild;
} else if (node.rchild == null) { // 右孩子为空,直接用左孩子替代
tmp = node.lchild;
} else { // 左右子树均不为空, 使用中序遍历的直接后继替代
Node preNode = null// 右子树中序遍历的第一个结点的双亲结点
,lnode = node.rchild; // 查找其右子树 中序遍历的第一个结点,其没有左孩子
while(lnode.lchild != null){
preNode = lnode;
lnode = lnode.lchild;
}
node.data = lnode.data; // 交换值
preNode.lchild = lnode.rchild; // 直接删除
tmp = node;
}
if(pre.lchild == node){
pre.lchild = tmp;
} else {
pre.rchild = tmp;
}
}
对于高度为H的二叉排序树,其插入和删除的运行时间都是O(H)。但在最坏的情况下,即构造二叉排序树的输入序列是有序的,就会形成一个倾斜的单枝树,此时二叉排序树性能显著变坏,树的高度也增加为元素个数N。
分析之前了解一下平均查找长度的概念。
为确定记录在查找表中的位置,与给定值进行比较的关键字的个数期望值称为查找算法在查找成功时的平均查找长度(ASL)。对于含有n个元素的查找表,查找成功的平均查找长度为:
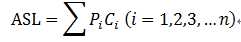
其中Pi为查找表中第i个元素的概率,Ci为找到第i个元素已经比较过的次数。
在查找表中找不到待查元素,但是找到待查元素应该在表中存在的位置的平均查找次数称为查找不成功的平均查找长度。
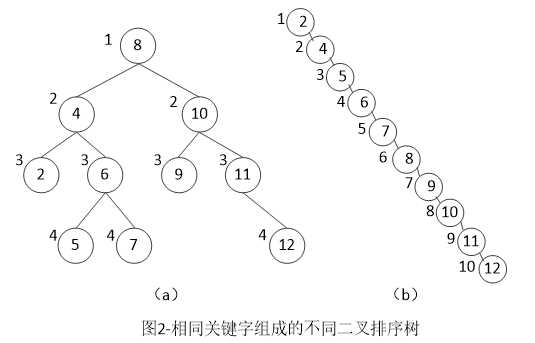
其中元素旁边的数字为查找成功时,比较的次数。
在等概率的情况下,图2(a)的查找成功的平均查找长度为(概率乘以关键字所在层数之和):
ASLa = (1+2+2+3+3+3+3+4+4+4)/10 = 2.9
而图2(b)的查找成功的平均查找长度为
ASLb=(1+2+3+4+5+6+7+8+9+10)/10=5.5
由上可知,二叉排序树查找算法的平均查找长度,主要取决于树的高度,与二叉树的形态有关。若二叉排序树是一个只有右(左)孩子的单枝树(类似于有序单链表),其平均查找长度和单链表相同,为O(n);若左右子树的高度差不超过1,即是平衡二叉树,其平均查找长度为O(log2n)。
二叉排序树与二分查找相似,就平均性能而言,它俩差不多,但二分查找的判定树唯一,而二叉排序树不唯一,不同的输入顺序,可能得到不同的二叉排序树。如上图。
针对维护表的有序性,二叉排序树无需移动结点,只需修改指针完成插入和删除,平均执行时间为O(log2n)。二分查找的对象是有序顺序表,插入和删除代价为O(n)。所以,若是静态查找表,宜用顺序表存储结构,用二分查找;若是动态查找表,则选择二叉排序树作为其逻辑结构。
标签:
原文地址:http://www.cnblogs.com/cyhe/p/5539023.html