标签:
堆排序
堆排序:基于优先队列的思想,时间复杂度为O(N logN )。
堆分为大顶堆和小顶堆,大顶堆是每个父节点的值都大于等于每个子节点的值,而小顶堆恰恰相反,每一个父节点的值都小于等于子节点的值。
首先是根据已知的数据构建一个大顶堆,给定的数组序列:a={16,7,3,20,17,8},构建过程如下:
根据给定的数组构建完全二叉树,
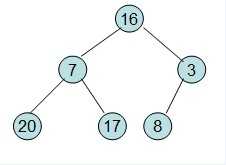
然后需要构造初始堆,则从最后一个非叶节点开始调整,调整过程如下:
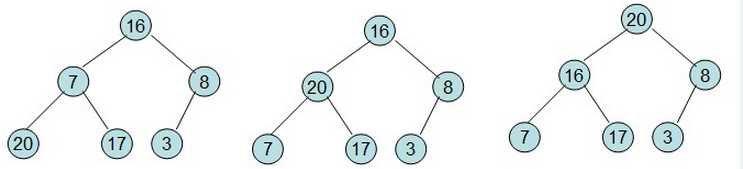
20和16交换后导致16不满足堆的性质,因此需重新调整:
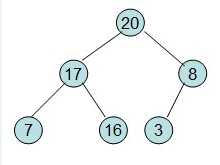
void percDown(int[] a, int i, int n){ int child; int tmp; for(tmp = a[i]; leftChild(i) < n; i = child){ child = leftChild(i); if(child < n -1 && a[child] < a[child + 1]) //如果右孩子大于左孩子 child++; if(tmp < a[child]) //孩子大于父节点 a[i] = a[child]; //将孩子节点的值赋值给父节点 else break; } a[i] = tmp; } int leftChild(int i){ //返回左孩子数组下标 return i * 2 + 1; } void build_Heap(int[] a){ for(int i = a.length/2; i>=0; i--) percDown(a,i,a.length); }
大顶堆构建完成,则需要每次取出根元素,将跟元素的值放入数组的末尾,就是将第一个数组元素和最后一个元素互换,然后将剩下的N-1个数组构建大顶堆,依次循环,构建大顶堆的数组为0。
void heapsort(int[] a){ build_Heap(a); for(int i = a.length -1; i > 0; i--){ int temp = a[0]; a[0] = a[i]; a[i] = temp; //交换第一个元素和最后一个元素的值 percDown(a,0,i); //数组前N-1个元素再次构建大顶堆 } }
标签:
原文地址:http://www.cnblogs.com/zhanglei93/p/5550314.html