标签:
排序算法有很多种,大家最先想到的大多是基于比较的排序吧,像冒泡排序、选择排序、插入排序都属此类。这些都是很容易想到的算法,它们的思想简单。但都有个缺点,就是比较慢,时间复杂度从O(n2)到O(Nlog(N))不等,在数据量小的时候还好,但应付大数据时就心有余而力不足了。
那有没有更快的算法呢?答案是肯定的,但我们需要换个角度思考,才能找到这些宝藏。前面已经讲了基于比较的排序算法时间复杂度都比较高,这个复杂度有一个下限O(Nlog(N)),想要更快,就必须突破这个下限。我们先假设有一个数组[5,4,1,2,3,4]
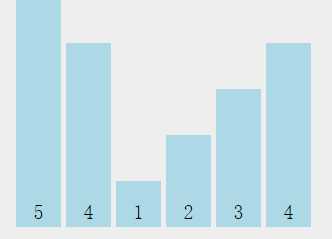
可以看到这个数组的值都为正整数(含负数的话改一下下限就可以了,道理一样的),最大值为5。如果有六个容器(暂且这么叫吧),分别给它们编号0-5
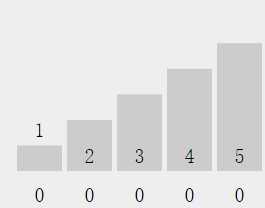
然后从先前数组中依次取出元素,放入编号和元素值相等的容器中。
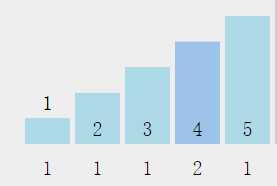
每个容器下面是它对应的元素的个数
这时,有没有感觉好像我们已经把元素排好序了?确实如此,最后一步很容易想到,
依次把元素取出来,放回原来的数组中,就成了这样:
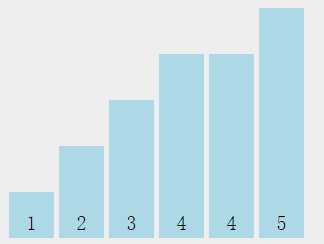
大功告成!这个就是传说中的更快的算法,它的时间复杂度为O(n),是线性的哦。这个算法的名字叫计数排序。
不过它也有个很明显的缺点,就是需要容器,在这里你可能还看不出这个有什么弊端,但如果这个数组最大的数是123456789,那么岂不是需要123456789个容器?很显然这是很严重的内存浪费。在数组为[123456789,5,4]这样的元素很少的情况下,浪费更是令人不忍直视。你可能会说可以写个子函数判断是不是有连续一大块容器没用,然后省去它们呀!这是个不错的想法,但有简单与美并存的更好的算法时,我们为什么要花大力气做这样一个复杂(可能还被你写的无比难看)的算法呢?
没错,我们下次要学习的就是这个简单优美的排序算法:基数排序,一字之差,效果可是千差万别呢。尽请期待!

是不是感觉被骗了呢?从头到尾一句代码都没有哈哈,这就对了,代码当然要自己写嘛,这个算法又不难。(saber之眼鄙视你)
参考文献与网站:《算法基础:打开算法之门》
http://zh.visualgo.net/(这可是个宝贝,一般人我都不告诉他嘻嘻~~)
标签:
原文地址:http://www.cnblogs.com/kirito-c/p/5559495.html