标签:
一.简述
二叉树的遍历主要是先序、中序、后序及对应的递归和非递归算法,共3x2=6种,其中后序非递归在实现上稍复杂一些。二叉树的遍历是理解和学习递归及体会栈的工作原理的绝佳工具!
此外,非递归所用的栈及相关操作是第三章实现的,但数据类型做了更改。
二.头文件

1 //3_1.h 2 /** 3 author:zhaoyu 4 email:zhaoyu1995.com@gmail.com 5 date:2016-6-7 6 note:realize my textbook <<数据结构(C语言版)>> 7 */ 8 //Page 46 9 #ifndef _3_1_FOR_CHAPTER6_H_ 10 #define _3_1_FOR_CHAPTER6_H_ 11 #include <cstdio> 12 #include <cstdlib> 13 #include "head.h" 14 /** 15 My Code 16 */ 17 #define SElemType BiTree 18 //----栈的顺序存储表示---- 19 #define STACK_INIT_SIZE 100//存储空间的初始分配值 20 #define STACKINCREMENT 10//存储空间分配增量 21 typedef struct{ 22 SElemType *base;//在栈构造之前和销毁之后,base 值为 NULL 23 SElemType *top;//栈顶指针 24 int stacksize;//当前已分配的存储空间,以元素为单位 25 }SqStack; 26 //----基本操作的函数原型说明及部分实现---- 27 Status InitStack(SqStack &S) 28 { 29 //构造一个空栈 S 30 S.base = (SElemType *)malloc(STACK_INIT_SIZE*sizeof(SElemType)); 31 if (!S.base) 32 { 33 exit(OVERFLOW); 34 } 35 S.top = S.base; 36 S.stacksize = STACK_INIT_SIZE; 37 return OK; 38 }//InitStack 39 40 Status StackEmpty(SqStack S) 41 { 42 //若 S 为空栈, 则返回 TRUE, 否则返回 FALSE 43 if (S.base == S.top) 44 { 45 return TRUE; 46 } 47 else 48 { 49 return FALSE; 50 } 51 } 52 53 Status GetTop(SqStack S, SElemType &e) 54 { 55 //若栈不空,则用 e 返回 S 的栈顶元素,并返回 OK; 56 //否则返回ERROR 57 if (S.top == S.base) 58 { 59 return ERROR; 60 } 61 e = *(S.top - 1); 62 return OK; 63 }//GetTop 64 Status Push(SqStack &S, SElemType e) 65 { 66 //插入元素 e 为新的栈顶元素 67 if (S.top - S.base >= S.stacksize) 68 {//栈满,追加存储空间 69 S.base = (SElemType *)realloc(S.base, 70 (S.stacksize+STACKINCREMENT)*sizeof(SElemType)); 71 if (!S.base) 72 { 73 exit(OVERFLOW); 74 } 75 S.top = S.base + S.stacksize; 76 S.stacksize += STACKINCREMENT; 77 } 78 *S.top++ = e; 79 return OK; 80 }//Push 81 Status Pop(SqStack &S, SElemType &e) 82 { 83 //若栈不空,则删除 S 的栈顶元素,用 e 返回其 84 //值,并返回OK;否则返回ERROR 85 if (S.top == S.base) 86 { 87 return ERROR; 88 } 89 e = *--S.top; 90 return OK; 91 }//Pop 92 #endif

1 //6_3_part1.h 2 /** 3 author:zhaoyu 4 date:2016-6-18 5 */ 6 #include "head.h" 7 #define TElemType char 8 //----二叉树的二叉链表表示---- 9 typedef struct BiTNode{ 10 TElemType data; 11 struct BiTNode *lchild, *rchild; 12 }*BiTree; 13 /** 14 algorithm 6.4 15 */ 16 Status CreateBiTree(BiTree &T) 17 {//按先序次序输入二叉树中结点的值(一个字符),空格字符表示空树 18 //构造二叉链表表示的二叉树 19 char ch; 20 scanf("%c", &ch); 21 if (‘ ‘ == ch) 22 { 23 T = NULL; 24 } 25 else 26 { 27 if (!(T = (BiTree)malloc(sizeof(BiTNode)))) 28 { 29 exit(OVERFLOW); 30 } 31 T->data = ch;//生成根结点 32 CreateBiTree(T->lchild); 33 CreateBiTree(T->rchild); 34 } 35 return OK; 36 } 37 Status Visit(TElemType e) 38 { 39 printf("%c", e); 40 return OK; 41 } 42 /** 43 algorithm 6.1 44 */ 45 Status RecursionPreOrderTraverse(BiTree T, Status (* Visit)(TElemType e)) 46 {//采用二叉链表存储结构,Visit是对数据元素操作的应用函数 47 //先序遍历二叉树 T 的递归算法 48 if (T) 49 { 50 if (Visit(T->data)) 51 { 52 if (RecursionPreOrderTraverse(T->lchild, Visit)) 53 { 54 if (RecursionPreOrderTraverse(T->rchild, Visit)) 55 { 56 return OK; 57 } 58 } 59 } 60 return ERROR;//这一行由于 Visit 函数只 return OK,貌似没什么用 61 } 62 else 63 { 64 return OK; 65 } 66 } 67 68 Status RecursionInOrderTraverse(BiTree T, Status (* Visit)(TElemType e)) 69 {//采用二叉链表存储结构,Visit是对数据元素操作的应用函数 70 //中序遍历二叉树 T 的递归算法 71 if (T) 72 { 73 if (RecursionInOrderTraverse(T->lchild, Visit)) 74 { 75 if (Visit(T->data)) 76 { 77 if (RecursionInOrderTraverse(T->rchild, Visit)) 78 { 79 return OK; 80 } 81 } 82 } 83 return ERROR; 84 } 85 else 86 { 87 return OK;//注意是 return OK; 88 } 89 } 90 Status RecursionPostOrderTraverse(BiTree T, Status (* Visit)(TElemType e)) 91 {//采用二叉链表存储结构,Visit是对数据元素操作的应用函数 92 //后序遍历二叉树 T 的递归算法 93 if (T) 94 { 95 if (RecursionPostOrderTraverse(T->lchild, Visit)) 96 { 97 if (RecursionPostOrderTraverse(T->rchild, Visit)) 98 { 99 if (Visit(T->data)) 100 { 101 return OK; 102 } 103 } 104 } 105 return ERROR; 106 } 107 else 108 { 109 return OK; 110 } 111 } 112 113 #include "3_1_for_chapter6.h" 114 Status UnRecursionPreOrderTraverse(BiTree T, Status (* Visit)(TElemType e)) 115 {//采用二叉链表存储结构,Visit是对数据元素操作的应用函数 116 //先序遍历二叉树 T 的递归算法 117 SqStack S; 118 BiTree p = T; 119 InitStack(S); 120 while (p || !StackEmpty(S)) 121 { 122 if (p) 123 { 124 if (!Visit(p->data)) 125 { 126 return ERROR; 127 } 128 Push(S, p); 129 p = p->lchild;//根指针进栈遍历做子树 130 } 131 else 132 {//根指针退栈,访问根结点,遍历右子树 133 Pop(S, p); 134 p = p->rchild; 135 } 136 } 137 return OK; 138 } 139 /** 140 algorithm 141 */ 142 Status UnRecursionInOrderTraverse_1(BiTree T, Status (* Visit)(TElemType e)) 143 {//采用二叉链表存储结构,Visit是对数据元素操作的应用函数 144 //中序遍历二叉树 T 的递归算法 145 BiTree p = NULL; 146 SqStack S; 147 InitStack(S); 148 Push(S, T);//跟指针进栈 149 while (!StackEmpty(S)) 150 { 151 while (GetTop(S, p) && p) 152 { 153 Push(S, p->lchild);//从左走到尽头 154 } 155 Pop(S, p);//空指针退栈 156 if (!StackEmpty(S)) 157 { 158 Pop(S, p); 159 if (!Visit(p->data)) 160 { 161 return ERROR; 162 } 163 Push(S, p->rchild); 164 } 165 } 166 return OK; 167 } 168 Status UnRecursionInOrderTraverse_2(BiTree T, Status (* Visit)(TElemType e)) 169 {//采用二叉链表存储结构,Visit是对数据元素操作的应用函数 170 //中序遍历二叉树 T 的递归算法 171 SqStack S; 172 BiTree p = T; 173 InitStack(S); 174 while (p || !StackEmpty(S)) 175 { 176 if (p) 177 { 178 Push(S, p); 179 p = p->lchild;//根指针进栈遍历做子树 180 } 181 else 182 {//根指针退栈,访问根结点,遍历右子树 183 Pop(S, p); 184 if (!Visit(p->data)) 185 { 186 return ERROR; 187 } 188 p = p->rchild; 189 } 190 } 191 return OK; 192 } 193 Status UnRecursionPostOrderTraverse(BiTree T, Status (* Visit)(TElemType e)) 194 {//采用二叉链表存储结构,Visit是对数据元素操作的应用函数 195 //后序遍历二叉树 T 的递归算法 196 //稍难一点 197 SqStack S; 198 BiTree p = T, pre = NULL; 199 InitStack(S); 200 Push(S, p); 201 while (!StackEmpty(S)) 202 { 203 if (GetTop(S,p) && p->lchild && pre!=p->lchild && !(p->rchild && pre == p->rchild)) 204 { 205 Push(S, p->lchild); 206 } 207 else if (p->rchild && pre!=p->rchild) 208 { 209 Push(S, p->rchild); 210 } 211 else 212 { 213 Pop(S, p); 214 if (!Visit(p->data)) 215 { 216 return ERROR; 217 } 218 pre = p; 219 } 220 } 221 return OK; 222 }
三.CPP文件

1 #include "6_3_part1.h" 2 int main(int argc, char const *argv[]) 3 { 4 BiTree T = NULL; 5 CreateBiTree(T); 6 printf("RecursionPreOrderTraverse\t"); 7 RecursionPreOrderTraverse(T, Visit); 8 printf("\n"); 9 printf("\n"); 10 printf("\n"); 11 12 printf("RecursionInOrderTraverse\t"); 13 RecursionInOrderTraverse(T, Visit); 14 printf("\n"); 15 printf("\n"); 16 printf("\n"); 17 18 printf("RecursionPostOrderTraverse\t"); 19 RecursionPostOrderTraverse(T, Visit); 20 printf("\n"); 21 printf("\n"); 22 printf("\n"); 23 24 printf("UnRecursionPreOrderTraverse\t"); 25 UnRecursionPreOrderTraverse(T, Visit); 26 printf("\n"); 27 printf("\n"); 28 printf("\n"); 29 30 printf("UnRecursionInOrderTraverse_1\t"); 31 UnRecursionInOrderTraverse_1(T, Visit); 32 printf("\n"); 33 printf("\n"); 34 printf("\n"); 35 36 printf("UnRecursionInOrderTraverse_2\t"); 37 UnRecursionInOrderTraverse_2(T, Visit); 38 printf("\n"); 39 printf("\n"); 40 printf("\n"); 41 42 printf("UnRecursionPostOrderTraverse\t"); 43 UnRecursionPostOrderTraverse(T, Visit); 44 printf("\n"); 45 printf("\n"); 46 printf("\n"); 47 return 0; 48 }
四.测试
测试用例(书的129页图6.9):
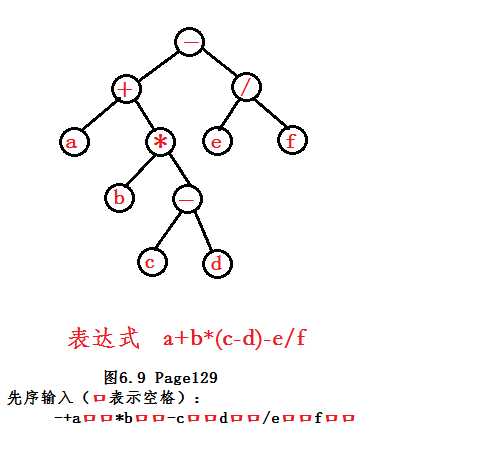
各种遍历表示
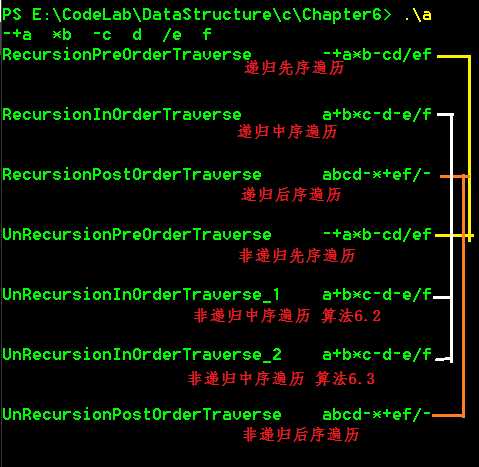
标签:
原文地址:http://www.cnblogs.com/zhaoyu1995/p/5575651.html