标签:
一、问题
给定两个字符串S和T,找出T在S中出现的位置。
二、朴素算法
当S[i] != T[j]时,把T往后移一位,回溯S的位置并重新开始比较。



(1) 成功匹配的部分(ABC)中,没有一样的字符
|
|
|
|
(2) 成功匹配的部分(ABA)中,有一样的部分(A)
|
|
|
|
三、KMP算法
通过整理模式串T中的元素相似性,减少朴素算法中对S不必要的回溯。
前缀:包含T首字母的子串
后缀:包含T最后一个字母的子串
next数组
next[j]: 求得T[0, ..., j-1] 中最长的相同的前/后缀,next[j] 是该前缀的后一个字符所在位置。当T[j] 和S[i]不相同时,回溯T[j] 到next[j],S[i]的位置不变。
(1) next[j] =-1 if j == 0 //第一个字符的回溯位置为 -1
(2) next[j] = max{k|T0...Tk-1 和 Tj-k-1...Tj-1} //最长的相同的前后缀,回溯时相同的部分不用再比较
(3) next[j] = 0 if 其他情况 //没有找到相同的前后缀,回溯的时候只能从第一个字符重新开始比较
计算next数组
T中有两个相同的子串X(蓝色部分),i 和 j 是当前比较的两个位置
(1) T[i] = T[j] = 2: next[j+1] = i+1 //T[0, ..., j] 的前缀Xi 和 后缀Xj 一样
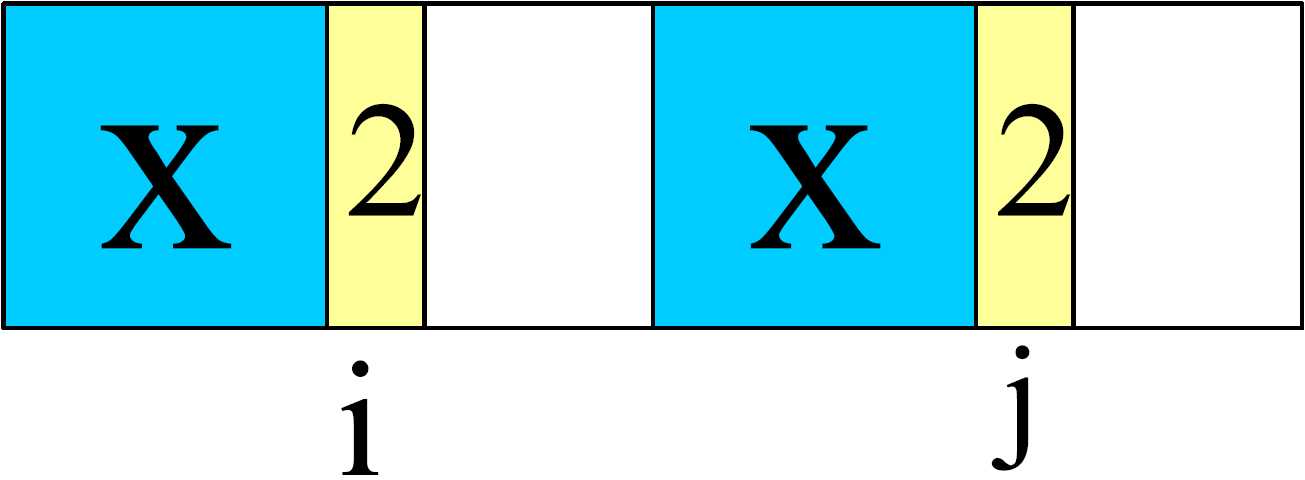
(2) 2 = T[i] != T[j] = 3: i = next[i] //对 i 进行回溯,重新寻找满足条件的前后缀。绿色部分,最后一个元素为 3

next数组的使用
(1) 成功匹配的部分(ABC)中,没有一样的字符
|
|
S[3] = D, T[3] = E, 不相同。j = next[3] = 0 回溯。(ABC)没有相同的部分,因此不必将 S:i 回溯再尝试匹配。
(2) 成功匹配的部分(ABA)中,有一样的部分(A)
|
|
S[3] = D, T[3] = C,第三个位置不匹配。j = next[3] = 1 回溯。下次比较是可以直接从S[3]和T[1]开始匹配,因为T[0] 和 T[2] 相同。
四、KMP算法源码
【hihocoder】 http://hihocoder.com/problemset/problem/1015?sid=808424

1 #include <iostream> 2 #include <string> 3 using namespace std; 4 5 //计算next数组 6 void get_next(string& T, int* next) 7 { 8 int i = 0, j = -1, Tlen = T.length(); 9 next[0] = -1; 10 while(i < Tlen) 11 { 12 if(j == -1 || T[i] == T[j]) 13 { 14 ++i; 15 ++j; 16 next[i]=(T[i] == T[j] ? next[j]:j);//使得回溯前和回溯后的元素不一样 17 } 18 else 19 j = next[j]; 20 } 21 } 22 23 //计算T在S中出现的次数 24 int subStrCnt(string& S, string& T) 25 { 26 int cnt = 0; 27 int Slen = S.length(), Tlen = T.length(); 28 int next[10000]; 29 int i = 0, j = 0; 30 get_next(T, next); 31 while(i < Slen && j < Tlen) 32 { 33 if(j == -1 || S[i] == T[j]) 34 { 35 ++i; 36 ++j; 37 } 38 else 39 j = next[j]; 40 if(j == Tlen){//T匹配完成,从T: next[j]再开始 41 cnt++; 42 j = next[j]; 43 } 44 } 45 return cnt; 46 } 47 int main() 48 { 49 int cnt; 50 string S, T; 51 cin>>cnt; 52 while(cnt-- > 0) 53 { 54 cin>>T>>S; 55 cout<<subStrCnt(S, T)<<endl; 56 } 57 return 0; 58 }
标签:
原文地址:http://www.cnblogs.com/coolqiyu/p/5596188.html