1 温习

1.1 关于caffe的名称：

caffe = convolutional architecture for fast feature embedding

1.2 caffe.proto

Protocol Buffers顾名思义这是一种协议接口，这是了解caffe功能之后，需要了解的第一件事情。有很多相关博客。简单看一下其结构：

package xx;#xx将作为名称空间 
message helloworld #定义类
 {                                #定义 filed
    required int32     xx = 1;  // 必须有的值 
    optional int32     xx = 2;  //可选值
    repeated  xx        xx=3; //可重复的
    enum xx {            #定义枚举类
        xx =1;
        } 
 }

1.3 caffe的结构：

caffe通过layer-by-layer的方式逐层定义一个网络，从输入到最终的输出判断从下而上的定义整个网络。他主要有blobs，layer，net等组成
1. blob Binary (Basic) Large Objects
blob存储整个网络中的所有数据（数据和导数），它是按c存储的连续n维数组，它在cup和GPU之间按需分配内存开销，通常为4维，某一坐标（n,k,h,w）的物理位置为（(n * K + k) * H + h) * W + w）
2. layer
每一个layer都定义了3种运算：
- setup：初始化时的设置及相互连接
- Forward：bottom–》top
3. Net
它是一种directed acyclic graph (DAG) 结构，使用 plaintext modeling language，简单的建立模型，简单的logistic模型如下：

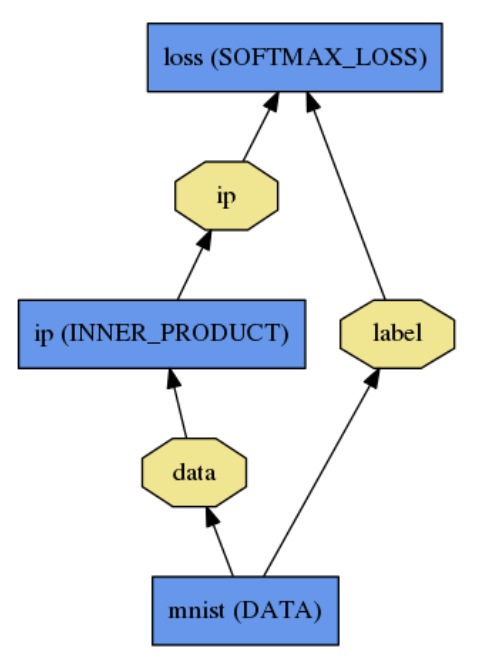
name:"logisticregression"
layer{
    name:"mnist"
    type:"Date"
    top:"data"
    top:"label"
    data_param{
      source:"yoursource"
      batch_size:yoursize
      }
}
layer {
    name:"ip"
    type:"InnerProduct"
    bottom:"data"
    top:"ip"
    inner_product_param{
      num_output:2
      }
}
layer {
    name:"loss"
    type:"SoftmaxWithLoss"
    bottom:"ip"
    bottom:"label"
    top:"loss"}

2 开始

LeNet是Yann LeCun（下方），facebook Ai 的director，1989年发表的文章中公布的，运用于美国支票手写字体。

下面是LeNet的结构，caffe使用的LeNet与原本稍有不同的是ReLU代替了softmax，计算简单，收敛快（请思考原因）。我们学习它的原因是虽然此网络比较简单但是包含了现在正在使用的大型网络的重点。

2.1 Data layer

layer{
    name:"mnist"
    type:"Date"#这里的type还有MemoryData(内存读取)HDF5Date，
               #HDF5output，ImageData等
    transform_param{
        scale:0.00390625#1/256
        }#预处理如减均值，尺寸变换，随机剪，镜像等
    data_param{
      source:"yoursourcepath"#必填
      backend:LMDB#默认为使用leveldb
      batch_size:64
    }
    top:"data"
    top:"label"
    }

2.2 convolutional layer

layer{
    name:"conv1"
    type:"Convolution"
    param{lr_mult:1}#weights的学习率与全局相同
    param{lr_mult:2}#biases的学习率是全局的2倍
    convolution_param{
      num_output:20#卷积输出数量
      kernel_size:5
      stride：1
      weight_filler{
         type:"xavier"}#一种初始化方法。
      bias_filler{
        type:"constant"}}#bias使用0初始化
    bottom:"data"
    top:"conv1"
    }

其中
type:”xavier”#一种初始化方法，这里有相关问题。
type:”constant”#bias使用0初始化，这里提到过 。

输入是（64，28，28）
卷积输出是（64，20，24，24）
参数为（20，1，5，5），（20，）
下图是卷积的计算过程

下一层是池化层

2.3 Pooling layer

layer{
    name:"pool1"
    type:"Pooling"
    pooling_param{
       kernel_size:2 
       stride:2 
       pool:MAX}
       bottom:"conv1" 
       top:"pool1"}

这里输出是（64，20，12，12），没有weight和biases

剩下还有两层卷积（num=50，size=5，stride=1）和池化层 ：

layer{
name:"conv2"
type:"Convolution" 
param:{lr_mult:1} 
param:{lr_mult:2} 
convolution_param{ 
   num_output:50 
   kernel_size:5 
   stride:1
   weight_filler{type:"xavier"}
   bias_filler{type:"constant"} 
bottom:"pool1" 
top:"conv2"}
} 
layer{
name:"pool2"
type:"Pooling"
bottom:"conv2"
top:"pool2"
pooling_param{
   pool:MAX
   kernel_size:2
   stride:2
 }
 }

卷积层输出是（64，50，10，10）
参数：（50，20，5，5）（50，）
池化层输出（64，50，5，5）
接下来是全连接层：

2.4 innerproduct layer

layer{
   name:"ip1"
   type:"InenerProduct"
   bottom:"pool2"
   top:"ip1"
   param:{lr_mult:1}
   param:{lr_mult:2}
   inner_product_param{
      num_output:500
      weight_fill{type:"axiver"}
      bias_fill{type:"constant"}
   }}

这里的输出（64，500，1，1）
参数（500，6250）（500，）

接下来是ReLu：

2.5 Relu layer

layer {
  name: "relu1"
  type: "ReLU"
  bottom: "ip1"
  top: "ip1"#底层与顶层相同减少开支
  #可以设置relu_param{negative_slope:leaky-relu的浮半轴斜率}
}

这里的输出（64，500）不变
下面是第二层ip

layer{
name:"ip2"
type:"InnerProduct"
bottom:"ip1"
top:"ip2"
inner_product_param{
   num_output : 10
   weight_filler{type:"xaiver"}
   bias_filler{type:"constant"}}}

输出为（64，10）
参数为（10，500）（10，）

下面就到了loss了：

2.6 loss layer

layer {
  name: "loss"
  type: "SoftmaxWithLoss"
  bottom: "ip2"
  bottom: "label"#终于用上了label，没有top
}

在原prototxt中我们还发现在datalayer中分类include{phase: TRAIN或者TEST}，而且在test中还有一层accuracy来计算准确率，它只有name,type,buttom,top,include{phase:TEST}几部分。

下面是整个过程：

下面几张ppt对于im2col介绍的挺好就放在这里了

2.7 im2col

2.8 solver

上面有了prototxt，现在还缺一个solver了，solver主要定义模型的参数更新与求解方法：

# 制定训练和测试模型
net: "your/prototxt.prototxt"
# 指定多少测试集参与向前计算，这里的测试batch size=100，所以100次可使用完全部10000张测试集.
test_iter:100
# 每训练test_interval次迭代进行一次训练.
test_interval： 500
# 基础学习率.
base_lr: 0.01
#动量
momentum: 0.9
#权重衰减
weight_decay: 0.0005
# 学习策略
#http://stackoverflow.com/questions/30033096/what-is-lr-policy-in-caffe
lr_policy:"inv"#inv: return base_lr * (1 + gamma * iter) ^ (- power)
gamma: 0.0001
power: 0.75
# 每display次迭代展现结果
display: 100
# 最大迭代数量
max_iter: 10000
# 保存临时模型的迭代书
snapshot: 5000
#模型前缀
#不加前缀为iter_迭代次数.caffemodel
#加之后为lenet_iter_迭代次数.caffemodel
snapshot_prefix: "examples/minst/lenet"
#设置求解其类型
solver_model：gpu

支持的求解器类型：

Stochastic Gradient Descent (type: "SGD"),
AdaDelta (type: "AdaDelta"),
Adaptive Gradient (type: "AdaGrad"),
Adam (type: "Adam"),
Nesterov’s Accelerated Gradient (type: "Nesterov") and
RMSprop (type: "RMSProp")

一篇好文章：
http://sebastianruder.com/optimizing-gradient-descent/
支持的lr_policy:
// - fixed: always return base_lr.
// - step: return base_lr * gamma ^ (floor(iter / step))
// - exp: return base_lr * gamma ^ iter
// - inv: return base_lr * (1 + gamma * iter) ^ (- power)
// - multistep: similar to step but it allows non uniform steps defined by 多了一个stepvalue：不同的步数
// stepvalue
// - poly: the effective learning rate follows a polynomial decay, to be
// zero by the max_iter. return base_lr (1 - iter/max_iter) ^ (power)
// - sigmoid: the effective learning rate follows a sigmod decay
// return base_lr ( 1/(1 + exp(-gamma * (iter - stepsize))))

主要参考：
1. http://caffe.berkeleyvision.org/gathered/examples/mnist.html
2. Tel Aviv University 特拉维夫大学caffe课程

2 python实现

这部分主要写了python下prototxt和solver的建立，建议大家都亲手实践下

2.1 设置prototxt

from pylab import *
%matplotlib inline
import caffe
import os
os.chdir(‘./caffe-rc3/examples‘)
from caffe import layers as L, params as P
def lenet(db_path,batch_size):#def的使用
    n=caffe.NetSpec()#注意caffe.netspec()
    n.data,n.label=L.Data(batch_size=batch_size,backend=P.Data.LMDB,source=db_path,
                          transform_param=dict(scale=1./255),ntop=2)
    n.conv1=L.Convolution(n.data,kernel_size=5,num_output=20,weight_filler=dict(type=‘xavier‘))
    n.pool1=L.Pooling(n.conv1,kernel_size=2,stride=2,pool=P.Pooling.MAX)
    n.conv2=L.Convolution(n.pool1,kernel_size=5,num_output=50,weight_filler=dict(type=‘xavier‘))
    n.pool2=L.Pooling(n.conv2,kernel_size=2,stride=2,pool=P.Pooling.MAX)
    n.fc1    =L.InnerProduct(n.pool2,num_output=500,weight_filler=dict(type=‘xavier‘))
    n.relu1=L.ReLU(n.fc1,in_place=True)
    n.score=L.InnerProduct(n.relu1,num_output=10,weight_filler=dict(type=‘xavier‘))
    n.loss=L.SoftmaxWithLoss(n.score,n.label)
    return n.to_proto()#n.to_proto最终输出
with open(‘/home/beatree/caffe-rc3/examples/traintry.prototxt‘,‘w‘) as f:
    f.write(str(lenet(‘/home/beatree/caffe-rc3/examples/mnist/mnist_train_lmdb‘,64)))
with open(‘/home/beatree/caffe-rc3/examples/testtry.prototxt‘,‘w‘) as f:
    f.write(str(lenet(‘/home/beatree/caffe-rc3/examples/mnist/mnist_test_lmdb‘,100)))
caffe.set_device(0)
caffe.set_mode_gpu()
solver=None

2.2 solver

solver 可以直接道入也可以在pyton下写

solver = caffe.SGDSolver(‘mnist/lenet_auto_solver.prototxt‘)#注意caffe.sgdsolver()

也可以自己写：

from caffe.proto import caffe_pd2
s=caffe_pb2.SolverParameter()
s.random_seed=0
#下面格式参数与之前在文本中看到的相似，只是：->=
#最后
with open(yourpath,‘w‘)as f:
    f.write(str(s))
然后与上面类似
solver=None
solver=caffe.get_solver(yourpath)

2.3 检查网络

2.3.1 检查输出shape

[(k, v.data.shape) for k, v in solver.net.blobs.items()]

得到

[(‘data‘, (64, 1, 28, 28)),
 (‘label‘, (64,)),
 (‘conv1‘, (64, 20, 24, 24)),
 (‘pool1‘, (64, 20, 12, 12)),
 (‘conv2‘, (64, 50, 8, 8)),
 (‘pool2‘, (64, 50, 4, 4)),
 (‘fc1‘, (64, 500)),
 (‘score‘, (64, 10)),
 (‘loss‘, ())]

2.3.2 检查参数shape

[(k, v[0].data.shape) for k, v in solver.net.params.items()]#注意都是solver.net.....

结果：

[(‘conv1‘, (20, 1, 5, 5)),
 (‘conv2‘, (50, 20, 5, 5)),
 (‘fc1‘, (500, 800)),
 (‘score‘, (10, 500))]

2.3.3 检查数据的载入

solver.net.forward() 
solver.test_nets[0].forward()  

得到一个结果
{‘loss’: array(2.365971088409424, dtype=float32)}
下面检查数据是否载入
训练集前8个图

imshow(solver.net.blobs[‘data‘].data[:8,0].transpose(1,0,2).reshape(28,8*28),cmap="gray");axis(‘off‘)
print ‘groundturth‘,solver.net.blobs[‘label‘].data[:8]

得到结果
：groundturth [ 5. 0. 4. 1. 9. 2. 1. 3.]

测试集八个图

imshow(solver.test_nets[0].blobs[‘data‘].data[:8,0].transpose(1, 0, 2).reshape(28,8*28));axis(‘off‘)
print ‘labels‘,solver.test_nets[0].blobs[‘label‘].data[:8]

labels [ 7. 2. 1. 0. 4. 1. 4. 9.]

2.4 运行一次

确定了我们载入了正确的数据及标签之后，开始运行solver，运行一个batch看是否有梯度变化

solver.step(1)
imshow(solver.net.params[‘conv1‘][0].diff[:,0].reshape(4,5,5,5).transpose(0,2,1,3).reshape(4*5,5*5),cmap=‘gray‘);axis(‘off‘)

(-0.5, 24.5, 19.5, -0.5)

2.5 最后的检查

最后我们自定义一个循环，查看网络运行是否稳定

%%time#上一篇文章使用的是%timeit
niter=200
test_interval=25
#预定义loss acc output 容器
train_loss=zeros(niter)
test_acc=zeros(int(np.ceil(niter/test_interval)))
output=zeros((niter,8,10))
for it in range(niter):
    solver.step(1)
    train_loss[it]=solver.net.blobs[‘loss‘].data
    solver.test_nets[0].forward(start=‘conv1‘)
    output[it]=solver.test_nets[0].blobs[‘score‘].data[:8]
    if it % test_interval ==0:
        print ‘iteration‘,it,‘testing...‘
        correct=0
        for test_it in range(100):
            solver.test_nets[0].forward()
            correct+=sum(solver.test_nets[0].blobs[‘score‘].data.argmax(1)==
#//得到的是商                         solver.test_nets[0].blobs[‘label‘].data)
        test_acc[it//test_interval]=correct/1e4

iteration 0 testing...
iteration 25 testing...
iteration 50 testing...
iteration 75 testing...
iteration 100 testing...
iteration 125 testing...
iteration 150 testing...
iteration 175 testing...
CPU times: user 19.4 s, sys: 2.72 s, total: 22.2 s
Wall time: 20.9 s

画出训练loss和测试accuracy

_,ax1=subplots()
ax2=ax1.twinx()
ax1.plot(arange(niter),train_loss)
#注意横坐标
ax2.plot(test_interval*arange(len(test_acc)),test_acc,‘r‘)
ax1.set_title(‘accuracy:{:.3f}‘.format(test_acc[-1]))

上面的结果开起来不错，下面我们再详细的看一下每个数字的得分是怎么变化的

for i in range(2):
    figure(figsize=(2,2))
    imshow(solver.test_nets[0].blobs[‘data‘].data[i,0],cmap=‘gray‘)
    figure(figsize=(20,2))
    imshow(output[:100,i].T,interpolation=‘nearest‘,cmap=‘gray‘)#output[:100,1].T前100次结果

下面的计算方式能够把低的分数和高的分数两极分化：

for i in range(2):
    figure(figsize=(2,2))
    imshow(solver.test_nets[0].blobs[‘data‘].data[i,0],cmap=‘gray‘)
    figure(figsize=(20,2))
    imshow(exp(output[:100,i].T)/exp(output[:100,i].T).sum(0),interpolation=‘nearest‘,cmap=‘gray‘)

最后一个是不是很明显呢？
现在我们得到了一个比较满意的网络，在之后我们还可以尝试作以下工作：
1. 定义新的结构（如加全连接层，改变relu等）
2. 优化lr等参数 （指数间隔寻找如0.1 0.01 0.001）
3. 增加训练时间
4. 由sgd–》adam
5. 其他