标签:
数据结构的一部分重要内容便是排序算法,排序之后可以采用快速的折半查找,排序算法多种多样,算法的度量标准主要有,1)稳定性,2)最好/坏情况下的时间复杂度,3)最好/坏情况下的空间复杂度。下图给出一个总结。
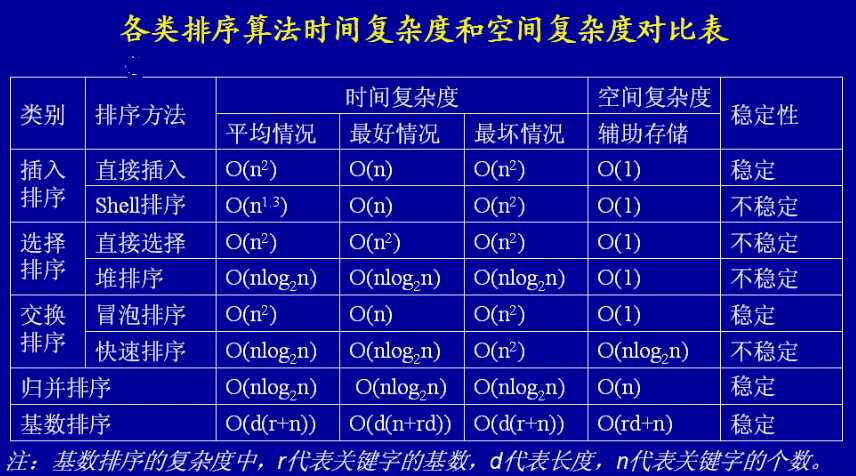
接下来引入常见的排序算法,及其性能分析,一下排序方法均是对于长度为 $n$ 的序列L进行排序,元素分别为 $(L_0,L_1,..L_{n-1})$ 。
1. 插入排序
1)直接插入排序 稳定,最好 $O(n)$ ,最差 $O(n^2)$ ,平均 $O(n^2)$ ,空间 $O(1)$
直接插入排序从待排序序列中选取一个数,选好一个位置将其插入到有序列表中,不断重复这个过程直到排序完成。

上图展示了直接插入执行的过程,开始假设 第 $0$ 个元素有序,对于第 $i=1...n-1$ 个元素,自 $i-1$ 起往前搜索,查找插入位置,同时后移记录,找到合适位置插入即可,可见共进行 $n-1$ 次插入,若数组有序只需进行 $n-1$ 次比较即可,无需移动,所示复杂度为 $O(n)$ ,若数组逆序,则需进行 $\frac{(n-1)(n-1+1)}{2}$ 次比较与移动,复杂度为 $O(n^2)$ ,所以 最好时间复杂度 $O(n)$ ,最差时间复杂度 $O(n^2)$ ,平均时间复杂度为 $O(n^2)$ 。由于在原地排序,空间复杂度为 $O(1)$ ,另外注意算法是稳定的。
2)折半插入排序
由于排序过程中前边已经有序,所以可以对有序序列进行折半查找,相对直接插入来说,减少了比较次数,但是由于找到插入位置后扔需移动序列中的元素,所以时间复杂度仍为 $O(n^2)$ 。
直接插入排序代码:

public void insert_sort(int[] nums){ if(nums == null || nums.length < 2) return; // i = 1 -> n-1 for(int i = 1 ; i < nums.length ; i ++){ if(nums[i] >= nums[i-1]) continue; int pivot = nums[i] ,j = i-1; // 待插入 while(j >= 0 && nums[j] > pivot) nums[j+1] = nums[j--]; nums[j+1] = pivot ; //j < 0代表插入到最掐面 } }
至于折半插入排序,需要用 binary search 找到插入位置插入即可。若有相同元素,为了保证其稳定性,则找到相同 key 的最后一个,比如说现在序列为 [1,1,1,1,1,3,4,1] ,我们要插入最后一个 1 ,为了保持其稳定性,则需找到最后一个 1 ,这种带有相同元素的 binary search 的代码如下:

public int binary_search(int[] nums,int POS, int key){ if(nums == null ) return -1; int low = 0; int high = nums.length -1; while(low <= high){ int mid = low + (high - low)/2; //防止溢出 if(nums[mid] == key){ if(POS == -1){ if(mid > 0 && nums[mid-1] == nums[mid]) high = mid-1; else return mid; }else if(POS == 1){ if(mid < nums.length-1 && nums[mid+1] == nums[mid]) low = mid +1; else return mid; }else return mid; // POS == 0 }else if(nums[mid]>key){high = mid -1 ;} else{low = mid + 1;} } return high; //在 high 之后的元素插入即可 }
2. 希尔排序
标签:
原文地址:http://www.cnblogs.com/ooon/p/5613902.html