《Linear Algebra and Its Application》-线性方程组的解

标签：

线性方程组的解：

  通过先前文章对矩阵方程、线性方程组和向量方程这三种方程的通解性的介绍，现在我们就可以比较简便的表达一个线性方程组了。即有如下形式：

  Ax = b。其中A是m x n的矩阵，对应线性方程组的系数矩阵，而x是R^n的一个向量，记录了n个未知量，b则是线性方程组等式右边的尝试，在这里本质上也是R^n的一个向量，那么基于这种表达形式，我们开始对线性方程组的解的结构进行讨论(类似于对于微分方程我们讨论其通解、特解的一个过程)。

  我们从b出发，无非面临如下的两种情况。

  齐次方程：

  b = 0(注意这里的0代表的是向量)。我们称这样的线性方程组为齐次方程组。

  即这里线性方程组可以写成Ax = 0的形式。很容易看到，这个方程必有一个解x0，其个个分量均为0，对应到线性方程组，即x1=0,x2=0,x3=0,…xn=0,在这里我们称这个解x0为平凡解。

  但这并不会影响我们求解齐次方程的解集，下面给出一个例子，进行对齐次线性方程组的解集进行讨论。(这里涉及一个向量的参数表达形式，很简单不必赘言)

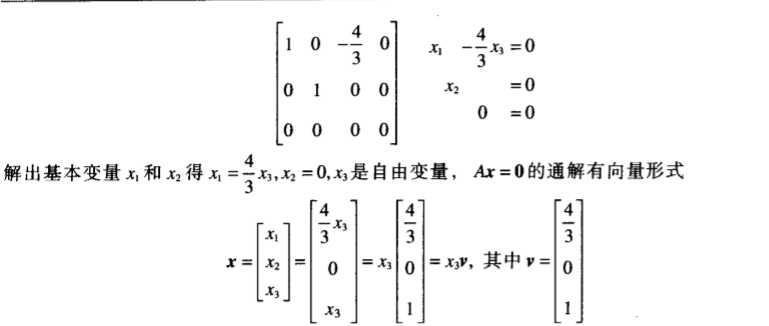
  非齐次方程：

  b≠0，我们基于上图给出的例题，给b一个非零向量的值再次进行求解。

  对比两个题目的答案，我们似乎有了惊喜的发现，在齐次方程的求解中，我们得到解用向量参数表达的形式为x = sv(s是常数，v是向量)，而在非齐次方程的求解中，我们得到的解用向量参数表达的形式为x = p + sv(s是参数，v、p是向量)，其实我们可以做更多的实验来检验，发现对于齐次方程组Ax = 0和非齐次方程组的解集，都存在上述形式上的规律，因此我们定义非齐次方程组的解集x = p + sv中的p是该方程组的特解，即有如下的定理成立。

 有意思的事，对于解是R^2或者R^3的情形，我们能够基向量的加法来从几何上描述这两组解的联系，即非齐次方程的组的任意解可以看成其特解向量p沿着对应齐次方程的任意解v平移任意个单位长度得到。

  从上面的例子中，我们不难在求解线性方程组的解集中添加一定的步骤使解集成为参数向量的形式。

  将相容方程组的解集写成参数向量的算法如下：

《Linear Algebra and Its Application》-线性方程组的解

标签：

原文地址：http://www.cnblogs.com/rhythmic/p/5615268.html