标签:
Lucas定理:
在组合计数问题中,我们常面临组合数C(n,m)过大而无法直接计算的困境,那么这里的Lucas定理给出了一个较大组合数进行取余运算的一种递归算法。
什么是Lucas定理?

Lucas定理的推导证明?

这个推导过程基于二项式定理,基于最后的等式,我们通过过找等是左边和右边x^(tp + r)的系数,即可完成对Lucas定理的证明。但是这里并没有呈现对p为什么是素数的说明。
在这里我们给出Lucas定理的另外一种表达形式:
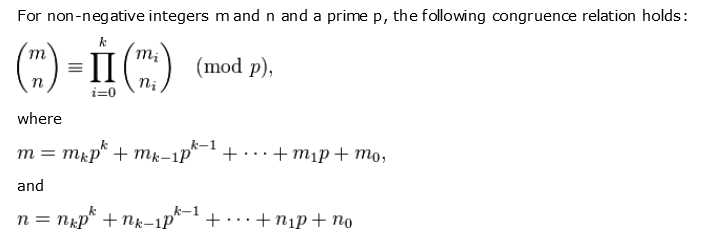
我个人认为,限定了取模的数p是素数,这样统一了运算,即对于∏中每个因子,C(mi,ni) % p的运算,我们都能够结合逆元和费马小定理来进行化简运算。
Lucas定理的编程实现?
通过上图Lucas的定义我们其实已经看到,它是一种递归调用的过程。
然后结合一个题目(Problem source : hdu 3037)来对其进行实现:
Q:给出变量n,m,p,求解x1+x2+x3+…xn = x的解的组数,x∈[0,m]。
分析:首先我们面临不存在空树的情况,利用基本的隔板原理(),容易得到C(m-1,n)组,这显而易见。但是问题的关键在于是允许空树存在的,因此我们需要另外选取空树的数量,即在选取的m-1个元素中再加n个树,在其中选择共选出n-1个空树和隔板,得到C(n+m-1,n-1)即C(n+m-1,m)。
则这道题目的最终解就是∑C(n+m-1,i) = C(n +m,m),i∈[1,m].(二项式系数恒等式,可以参见《具体数学》)
下面是编程实现。
#include <iostream> #include <cstdio> #include <cstring> using namespace std; const int N =150000; long long n, m, p, fac[N]; void init() { int i; fac[0] =1; for(i =1; i <= p; i++) fac[i] = fac[i-1]*i % p; } long long pow(long long a, long long b) { long long tmp = a % p, ans =1; while(b) { if(b & 1) ans = ans * tmp % p; tmp = tmp*tmp % p; b >>=1; } return ans; } long long C(long long n, long long m) { if(m > n) return 0; return fac[n]*pow(fac[m]*fac[n-m], p-2) % p; } long long Lucas(long long n, long long m) //C(n,m) % p { if(m ==0) return 1; else return (C(n%p, m%p)*Lucas(n/p, m/p))%p; } int main() { int t; scanf("%d", &t); while(t--) { scanf("%I64d%I64d%I64d", &n, &m, &p); init(); printf("%I64d\n", Lucas(n+m, m)); } return 0; }
标签:
原文地址:http://www.cnblogs.com/rhythmic/p/5617693.html