标签:
堆的定义如下:n个元素的序列(K1,K2......Kn)当且仅当满足Ki<=K2i&&Ki<=K2i或Ki>=K2i&&Ki>=K2i(i=1,2,3,...n/2)时称之为堆
以一维数组作为堆的存储结构,堆可以看成一个完全二叉树。
最大堆:每个父节点的都大于孩子节点。
最小堆:每个父节点的都小于孩子节点。
1、建堆:一个无序序列int a [] = {0,1, 3, 2, 5, 4};//其中红色的数字表示数组下标
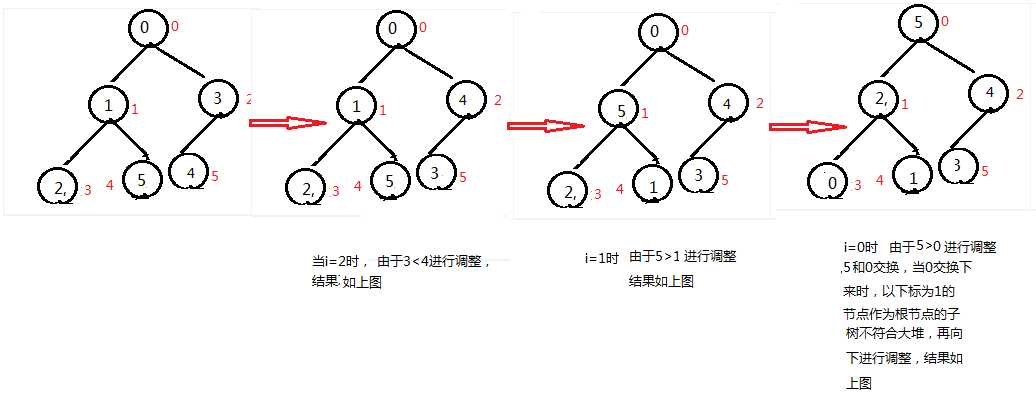
//建大堆
Heap(const T*a, size_t size) { for (size_t i = 0; i < size; ++i) { _array.push_back(a[i]); } for (int i = (_array.size() - 2) / 2; i>0; --i)//第一个非叶子结点,及上图的结点3 { AdjustDown(i); } } void AdjustDown(int root) { int child = root * 2+1; while (child < _array.size()) { if (child + 1 < _array.size() && _array[child + 1] > _array[child]) { ++child; } if (_array[child] > _array[root]) { swap(_array[child], _array[root]); root = child; child = 2 * root + 1; } else { break; } } }
2、堆排序
堆排序在最好和最坏情况下时间复杂度都为O(N*lgN),空间复杂度为O(1),由上面建堆的过程可知堆排序只适用于与可以支持随机访问的序列,如数组如果是链表的排序就不可以使用堆排序。
思想:如果要排位升序,则要建大堆,则每次位于堆顶的元素就为最大值,与堆上的最后一个结点交换即数组的最后一个元素,交换后再对除最后一个元素以外的数进行调整,再将此次范围中的堆顶元素与此次范围中的最后一元素进行交换,以此进行下去直至有序。
void AdjustDown(int * a, size_t size, int root)//建大堆 { assert(a); int child = 2 * root + 1; while (child < size) { if (child + 1 < size) { if (a[child] < a[child + 1]) ++child; } if (a[root] < a[child]) { swap(a[child],a[root] ); root = child; child = 2 * root + 1; } else { break; } } } void HeapSort(int * a, size_t size) { assert(a);
assert(size>0);
if(size<2)
{
if(a[0]>a[1])
{swap(a[0],a[1]);}
} for (int i = (size - 2) / 2; i >= 0; --i) { AdjustDown(a, size, i); } for (int i = size - 1; i > 0; --i) { swap(a[0], a[i]); AdjustDown(a, i, 0); } }
标签:
原文地址:http://www.cnblogs.com/Blog-day/p/My_Blog_Days_18.html