标签:
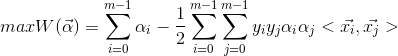


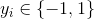

由于该矩阵是对称矩阵,因此在内存中的占用空间可以为m(m+1)/2
映射关系为:

既然α值是变量,因此对α值进行求导,后面根据梯度选取α值进行优化。
梯度:

若使W最大,则当α减少时,G越大越好。反之,G越小越好。
每次选取2个α值进行优化,其它α值视为常数,根据约束条件 得:
得:



进行优化之后:

由于α的范围在区间[0,C],所以△α受α约束
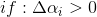
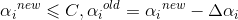




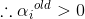

若选取的 和
和 异号,即λ=-1,则
异号,即λ=-1,则 和
和 增减性相同
增减性相同
假设 ,
,
若 ,则
,则 ,此时应选取
,此时应选取
上述命题可化为(注: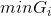 与
与 等价)
等价)


若选取的 和
和 同号,即λ=1,则
同号,即λ=1,则 和
和 增减性相异
增减性相异
若 ,则
,则 ,此时应选取
,此时应选取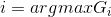 ,
,
上述命题可化为(注: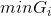 与
与 等价)
等价)


或

将上述结论进行整理,可得(为了简便此处只选取G前的符号与y的符号相异的情况)
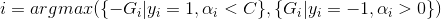
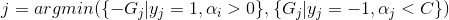
alpha要求在区间[0,C]内,对不符合条件的alpha值进行调整,调整规则如下。
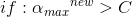


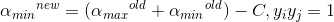

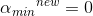

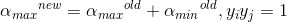
分2种情况,若λ=-1,即:

代入后得:

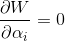

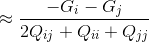
若λ=1,即:


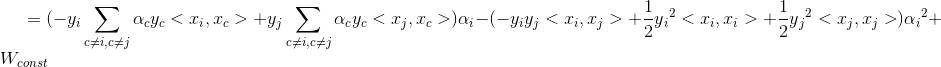
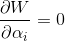


然后进行梯度调整,调整公式如下:
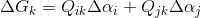
计算公式如下:


标签:
原文地址:http://www.cnblogs.com/fanwenjie/p/5657768.html