标签:
本篇博文讲述基因算法(Genetic Algorithm),基因算法是最著名的进化算法。
内容依然来自博主的听课记录和教授的PPT。
Holland‘s早期的基因算法被认为是“简单的基因算法”或是“权威的基因算法”。(simple genetic algorithm or canonical genetic algorithm)
问题描述:利用遗传算法求解区间[0,31]上的二次函数y=x2的最大值
乍一看,是个很白痴的问题,那我们就用GA算法来套一下,看一下流程。
[0, 31] 中的点x就是个体(individual), 函数值f(x)恰好就可以作为x的适应度(fitness),区间[0, 31]就是一个种群(population) 。
种群规模设定为4,用5位二进制数编码染色体。
假定4个个体:
S1: 13 = 01101(二进制)
S2: 24 = 11000
S3: 8 = 01000
S4: 19 = 10011
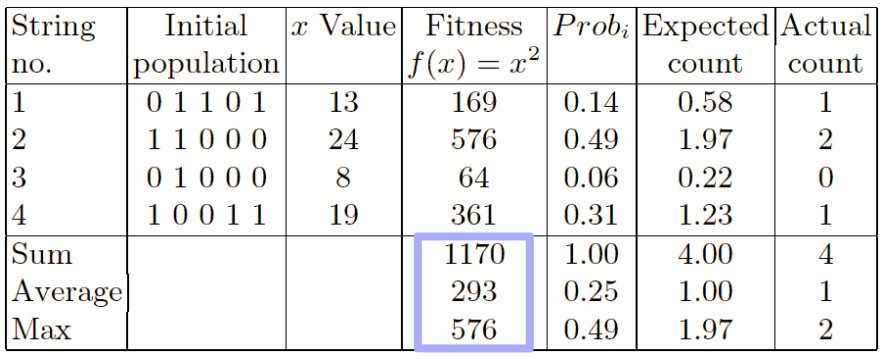
第一列是编号,第二列是初始值的二进制值(initial population),第三列就是给定的初始值,第四列f(x) = x^2是适应度(fitness),当然适应度越高越符合预期。第五列是种群中各个体的选择概率(prob)(根据第四列能算出来的)。第七列是个体在配对池(mating pool)中的个数。
选择概率的计算公式为:
![]()
下面开始重组配对(crossover):
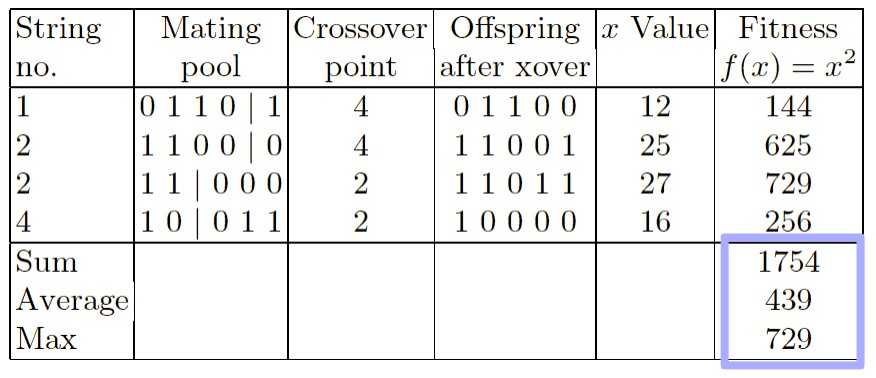
上图表格是配对重组的过程。第一列依然是编号,第二列是配对池,第三列表示重组开始的点,第四列是配对重组后的后代,第五列是新的后代的值,第六列是适应度。
下面是变异(mutation):
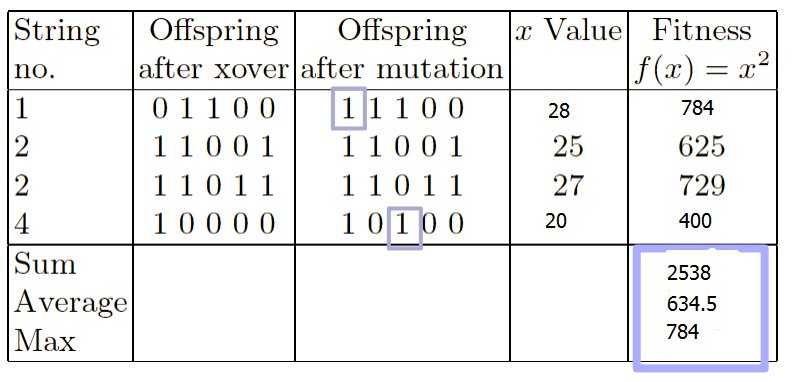
前两列内容和之前的一样,第三列是变异后的二进制值,编号1的个体在第一位发生了变异,编号4的个体在第三位发生了变异。数值发生了改变,适应度也发生了变化。
注:这里博主把教授的ppt给改了一下,因为博主不认为他原来写的数值是正确的。原数值如下:在S1的第四列,原ppt上的数字是26,第五列的数字是676。在S4的第四列,原ppt上的数字是18,第五列上的数字是324。当然下面的总和、平均值、最大值也都全部改了。
有一个问题,为什么变异了第一个和第四个,而第二个却没有变异呢?计算机是如何判断让哪一个个体进行变异的呢?
这里讲一个概念叫变异率(mutation rate),这是一个固定的值,在这个问题中我们设变异率0.001,也就是事先告诉计算机的一个数值。在基因的每一位上,也就是二进制码的每一位上,计算机会产生一个随机数,范围在[0,1]之间。接着计算机会将这个随机数与变异率进行比较,如果这个随机数小于这个变异率,那么在这一位上的基因将会发生反转。从这个变异的结果上来看,变异是朝着好的方向进行的。
至此一轮的进化已经走完了,可以看到新的后代:
S1: x = 28, f(x) = 784
S2: x = 25, f(x) = 625
S3: x = 27, f(x) = 729
S4: x = 20, f(x) = 400
可以对比一下第一张表格和最后一张表格,平均适应度由开始的293增加到了634.5,最适应的种群有最开始的576增长到了784。当然最终最好的、我们想要的结果是31^2 = 961。
此外再补充一个教授ppt上的表格
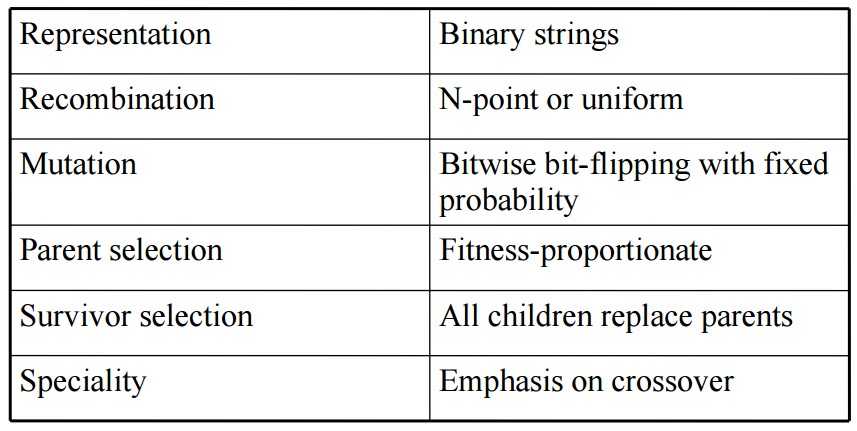
缺点总结:
二进制表达是最简单的表达方式之一。比如上面的那个问题就是用的二进制表达。
对于一个给定的问题,我们需要决定: 1.string的长度。2.如何用它来表示一个表型(phenotype)。
具体来说,我们需要保证,我们的每一个二进制编码都能够表示一个有效的solution,反之亦然,所有可能的solution都可以被表达。
教授的原文:In choosing the genotype-phenotype mapping for a specific problem, one has to make sure that the encoding allows that all possible bit strings denote a valid solution to the given problem and that, vice versa, all possible solutions can be represented.
主要先拿二进制表达开刀,其他的表达先略过。
除了二进制表示,还有一些其他表达方法,列举如下:
有些问题并不总适用于二进制表示。比如在一个正方形网格地图上寻找路径的过程中,我们可能会使用整型{0,1,2,3}来表示方向{东,南,西,北}。这里显然整型会比二进制更加合适。
变异本来是个生物学的名词,这里就是表明变异算子(variation operators)通过对基因型的一些随机变化,仅仅用一个父辈创造出了一个新的后代。
原文如下:Mutation is the generic name given to those variation operators that use only one parent and create one child by applying some kind of randomised change to the representation(genotype).
在最开始的例子中已经演示过二进制表达的变异。
最常见的二进制变异就是考虑每一位上的基因是否反转(从1到0,从0到1),这个反转有一个极小的概率pm。
主要先拿二进制表达开刀,其他的表达先略过。
重组被认为是基因算法中最重要的特征之一。
重组的概念上一章讲过了,这里引一段教科书的描述。
Recombination, the process whereby a new individual solution is created from the information contained within two (or more) parent solutions, is considered by many to be one of the most important features in genetic algorithms(GA).
这里重组的概念,有时候会说recombination,有时候会说crossover。crossover更常用来表示two-parent case。
重组算子(Recombination operators)的使用中会有一个重组率(crossover rate),这个概率的取值范围大约是[0.5,1.0]。通常在重组的过程中,一个位置上发生重组的概率会在[0,1),然后这个概率再和上面的我们实现设定好的重组率进行比较,倘若这个值低于了重组率,那么两个父辈就会通过重组产生两个新的后代。相反,则不发生重组,两个新的后代通过无性生殖(asexually)产生。也就是说,在经过一轮重组之后,有一部分后代(offspring)是直接copy父辈而产生的,另有一部分后代表达了之前没有见过的solutions。
回顾一下重组率(crossover rate)和变异率(mutation rate)
变异率(mutation rate)是用来控制染色体的一些部分如何独立地发生变化。所谓独立就只需要一个父辈就可以了。
重组率(crossover rate)决定了一组父辈发生重组的机会。
4.1.1 单个位置的交叉重组(One-Point Crossover)
从某一个位置开始进行交叉重组。

4.1.2 多个位置的交叉重组(N-Point Crossover)
从不止一个位置开始进行交叉重组。
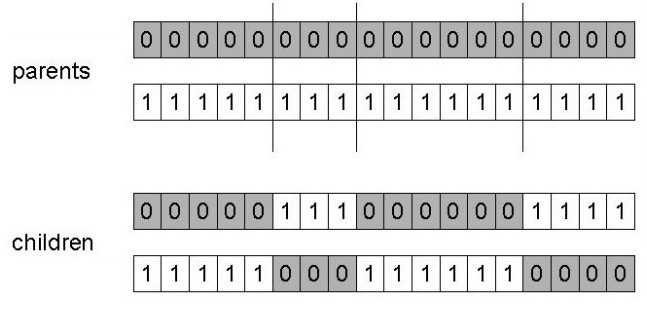
这两个划分看上去有点多余,但人家西方教科书就这么区分开了。
4.1.3 均衡交叉重组(Uniform Crossover)
与上面两种方式不同的是,uniform crossover这种重组方式是不依赖于基因的具体位置的。它首先在[0,1]上产生一组均匀分布的随机变量,组成一个string,其长度和父辈基因相同。然后有一个事先设定好的参数p(通常是0.5)。在第一个后代的每一位上,如果这个随机变量小于了这个参数,那么后代就遗传第一个父辈的基因,反之,如果这个随机变量大于了这个参数,那么后代就遗传第二个。第二个后代的基因则和第一个后代的重组方式完全相反。
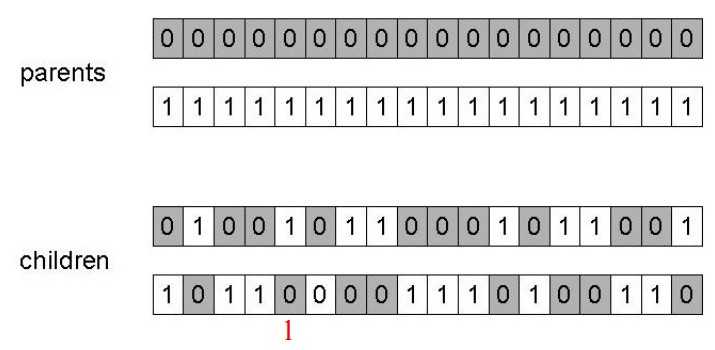
以上三种方式的小结和补充
n-point crossover倾向于将位置接近的基因保持在一起。这种效果被称为位置偏向(positional bias)
相反,uniform crossover没有任何的positional bias。他能够从每个父辈那里传递50%的基因并且防止单从某一个父辈那里获得大量的基因。这种效果被称作分布偏向(distributional bias)。
主要先拿二进制表达开刀,其他的表达先略过。
2. Genetic Algorithm(1) ——进化算法
标签:
原文地址:http://www.cnblogs.com/adelaide/p/5659946.html