标签:
嘛嘛嘛,好像大家在实现Kruskal算法是都是用的边集数组,判断图的连通性咱不会,o(╯□╰)o(为什么咱这么菜诶)
Kruskal算法:
规则:
(1)对每一条边按照从小到大进行排序
(2)加入边的时候判断这条边与之前的边是否构成回路,如果构成则放弃这条边,否则就加入到最小生成树中
边集数组:
struct Edge{ int begin; int end; int weight; };
起点,终点,权值,这些都好懂的。
然后判断是否构成回路则是采用了并查集的思想:大家如果不懂并查集,可以看看这篇博客:并查集详解这篇博文,当初就是看这篇博文入门的(博客园咋插入超链接呢?o(╯□╰)o)
设置一个Parent[]数组,
int Parent(int f){ while(parent[f]){ f=parent[f]; } return f; }
这是判断是否构成回路的函数
最后就是整个代码:
#include <algorithm> #include <iostream>
using namespace std; const int MAXSIZE=100; struct node{ int begin; int end; int weight; }Gnode[MAXSIZE]; int parent[MAXSIZE]; int Parent(int f){ while(parent[f]){ f=parent[f]; } return f; } int cmp(node s1,node s2){ return s1.weight<s2.weight; } void Kruskal(node p[],int k){ int n,m; for(int i=1;i<=MAXSIZE;i++){ parent[i]=0; } sort(p,p+k,cmp); for(int i=1;i<=k;i++){ n=Parent(p[i].begin); m=Parent(p[i].end); if(n!=m){ cout<<‘V‘<<p[i].begin<<" "<<‘V‘<<p[i].end<<" "<<p[i].weight<<endl; parent[n]=m; } } } int main(){ cout<<"Kruskal算法求最小生成树"<<endl; cout<<"请输入图的边数"<<endl; int num; cin>>num; for(int i=1;i<=num;i++){ cin>>Gnode[i].begin>>Gnode[i].end>>Gnode[i].weight; } cout<<"最小生成树的每条边级其权值"<<endl; Kruskal(Gnode,num); return 0; }
附上测试数据:
10 1 2 6 1 3 1 1 4 5 2 3 5 2 5 3 3 4 5 3 5 6 3 6 4 4 6 2 5 6 6
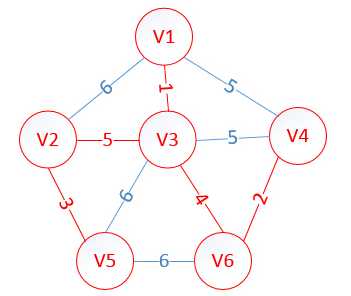
这是最后构建出的最小生成树
标签:
原文地址:http://www.cnblogs.com/mlgjb/p/5670048.html