遗传算法在JobShop中的应用研究（part 1）

标签：

 1. 什么是JobShop问题

1. Job,中文翻译成工件。一个工件又由若干道工序加工完成。
2. resource, 资源。在本文的车间调度中资源指的是机器，每道工序要在某个特定机器上加工。
3. Constraint, 约束。在车间调度中约束主要有以下两种：
   1. 同一个工件包含的工序有先后顺序。
   2. 每个机器不能同时处理两道工序，因此这台机器上完成工序时要串行，不能并行。
4. Objective,目标。JobShop问题的一个常见目标是使所有工件完成的总时间最小，这个总时间英语叫做Makespan。

一个JobShop问题可以用一个表格来刻画，例如下面的表格：

θ表示工序，例如， θ(1,1)就表示第1个工件的第1道工序。

r (i,j)表示机器编号，例如，r(1,1)=1,表示第一个工件的第一道工序的加工机器号为1。

D (i,j) 表示加工时间，例如，D(1,1)=3，表示第一个工件的第一道工序的加工需要3个单位的时间。

 JobShop问题的一个解可以用一个加权有向无环图来表示，请看下面的一个有向无环图：

     这个加权有向无环图就代表上述JobShop问题的一个解，我们可以看到每个工序作为图中的一个节点出现，权重就是这个节点对应的加工时间。工序之间的先后顺序用箭头表示，在这里需要注意的是：除了同一个工件下面的工序之间有先后顺序外，同一台机器上加工的工序也要串行。另外，我们增加了两个虚节点，分别为 θI 和 θF,表示开始和结束。从θI有箭头指向每个工件的第一道工序，从每个工件的最后一道工序出发用箭头指向 θF。虚节点的加工时间为0。

    一个有向无环图中有若干条从θI到θF的路径，在这些路径中我们找出那条路径上所有节点的权重相加最大的那一条，这个最大的权重和就是这个解对应的makespan,即所有工件加工完毕所需的时间。

 2. 遗传算法与JobShop

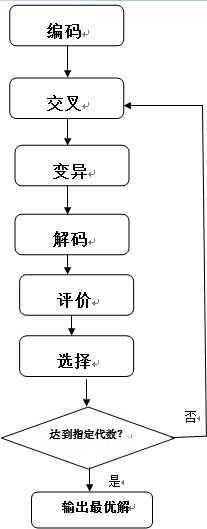
遗传算法是一种随机搜索算法，它主要分为六大功能模块：编码、交叉、变异、解码、评价、选择。整个算法的流程如下:

1. 编码：

      我们利用工件号的排列来表示工序的先后顺序，例如：1212这个排列中第一个1代表第一个工件的第一道工序，第二个1代表第一个工件的第二道工序，第一个2代表第二个工件的第一道工序，第二个2代表第2个工件的第二道工序。可见，1212这个排列可以完全体现出上面的有向无环图中体现的节点先后顺序。

    需要说明的是一个有向无环图可能对应多个工件号的排列方式，例如，1212,2121,1221,2112都对应上面的有向无环图。

    在遗传算法中首先做的就是编码，即随机生成若干个工件号的排列，这些个随机生成的排列构成的集合被称为种群，每个排列被称为染色体。

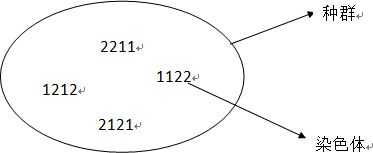
 如图所示，种群大小为4，该种群中包含4条染色体，分别为2211,1212,1122,2121。请思考为什么1111为非法染色体？

遗传算法在JobShop中的应用研究（part 1）

标签：

原文地址：http://www.cnblogs.com/zhaogeatdlnu/p/5668271.html